KMP算法

暴力匹配法(bad)

假设现在str1匹配到 i 位置，子串str2匹配到 j 位置，则有:

  1. 如果当前字符匹配成功（即str1[i] == str2[j]），则i++，j++，继续匹配下一个字符
  2. 如果失配（即str1[i]! = str2[j]），令i = i - (j - 1)，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。
  3. 用暴力方法解决的话就会有大量的回溯，每次只移动一位，若是不匹配，移动到下一位接着判断，浪费了大量的时间。

暴力匹配代码实现

ViolenceMatch

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package com.yukinoshita.algorithm.kmp;

public class ViolenceMatch {
    public static void main(String[] args) {
        String s1 = "yukinoYukinoShiTAyukinoYukinoshitaYukino";//23
        String s2 = "YukinoshitaYukino";
        int index = violenceMatch(s1,s2);
        System.out.println(index);
    }

    //暴力匹配算法实现
    public static int violenceMatch(String str1, String str2) {
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();

        int len1 = s1.length;
        int len2 = s2.length;

        int i = 0;//指向s1的索引
        int j = 0;//指向s2的索引
        while(i<len1 && j<len2) {
            if(s1[i] == s2[j]) {
                i++;
                j++;
            }else{//没有匹配成功
                i = i-(j-1);
                j=0;
            }
        }

        if(j==len2){
            return i-j;
        }else{
            return -1;
        }
    }
}

KMP算法

KMP算法介绍

  1. KMP是一个解决模式串在文本串是否出现过，如果出现过，最早出现的位置的经典算法
  2. Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法
  3. KMP方法算法就利用之前判断过信息，通过一个next数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过next数组找到，前面匹配过的位置，省去了大量的计算时间
  4. 参考blog

示例-字符串匹配问题

  1. 有一个字符串 str1= “BBC ABCDAB ABCDABCDABDE”，和一个子串 str2=“ABCDABD”
  2. 现在要判断 str1 是否含有 str2, 如果存在，就返回第一次出现的位置, 如果没有，则返回-1
  3. 要求：使用KMP算法完成判断，不能使用简单的暴力匹配算法

详细思路

最详细的见此：blog

以str1 = "BBC ABCDAB ABCDABCDABDE"以及str2 = "ABCDABD"进行举例，判断str1中是否含有str2。

  1. 首先，用str1的第一个字符与str2的第一个字符比较，发现不匹配，则关键词后移一位

    image-20241112093421135

  2. 再往后比较，不匹配则一直重复步骤1

    image-20241112093602904

  3. 重复步骤1，直到找到str1中和str2的第一个字符匹配（如下：）

    image-20241112093800648 image-20241112093851050 image-20241112093929032

  4. 之后方别移动i和j，比较两个str1与str2的重合度，发现当子串到最后的'D'时与源字符串的' '不匹配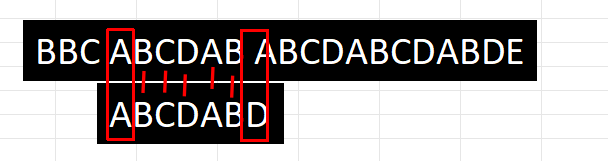

    image-20241112094320306

  5. 之后就是与暴力匹配有所区别的地方，不能简单地再让子串第一个字母A与源字符串的’B’、‘C’、‘D’进行比较，这些步骤都是浪费的，因为第4步其实已经比较过"BCD"了，我们知道了子串的第一个字符’A’不可能与’B’、‘C’、'D’匹配上。更准确说，当str1的空格与str2的’D’不匹配时，我们已经遍历过str1中的"ABCDAB"，所以正确地做法是将子串直接移动到下一个’A’的位置，这样子做才能提升搜索效率，而不要再让B与A比较

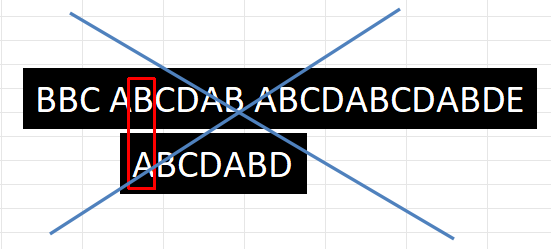
    image-20241112130246079

  6. 怎么样能把这些重复步骤省略呢？我们可以对子串str2计算部分匹配表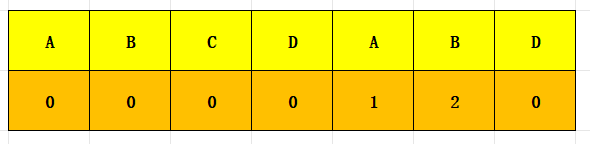

    image-20241112151917543
    • 如何得到部分匹配表？
    • 先介绍前缀与后缀，例如字符"yukino"，前缀就是"y"、“yu”、“yuk”、“yuki”、“yukin”；后缀就是"o"、“no”、“ino”、“kino”、“ukino”
    • 部分匹配值：一个字符串前缀和后缀共有元素的最大长度，回到"ABCDADB"这个例子：
      • "A"前缀和后缀都为空，所以部分匹配值为0
      • “AB"的前缀是"A”，后缀是"B"，所以部分匹配值为0
      • “ABC"的前缀是"A”、“AB”，后缀是"B"、“BC”，所以部分匹配值为0
      • “ABCD"的前缀是"A”、“AB”、“ABC”，后缀是"D"、“CD”、“BCD”，所以部分匹配值为0
      • “ABCDA"的前缀是"A”、“AB”、“ABC”、“ABCD”，后缀是"A"、“DA”、“CDA”、“BCDA”，所以部分匹配值为1
      • “ABCDAB"的前缀是"A”、“AB”、“ABC”、“ABCD”、“ABCDA”，后缀是"B"、“AB”、“DAB”、“CDAB”、“BCDAB”，所以部分匹配值为2
      • 同理，"ABCDABD"的部分匹配值为0
    • 这样就能从理论层面，知道如何得到部分匹配值表。（关键是看代码怎么实现——利用next数组）

  7. 那么这个表怎么用呢？回到刚才str1中的空格与str2中的D不匹配的时刻，此时前六个字符"ABCDAB"是匹配的，最后一个字符"B"对应的"部分匹配值"为2，因此按照如下公式移动步数：
    $$
    移动位数=已匹配的字符数-部分匹配值
    $$
    因此此时移动的步数为：$6-2=4$步，如下所示：

    image-20241112131045712

  8. 下一次发现，空格与字符C又不匹配，同样根据公式计算，需移动$2(已匹配字符数)-0(第一个字符’B’所对应的部分匹配值)=2$步：

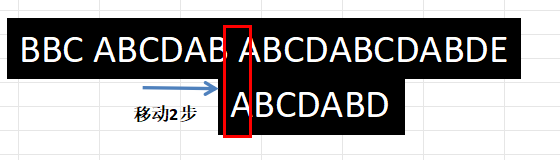
    image-20241112131333017 image-20241112131418061

  9. 后续步骤同理，不再说明，下图匹配成功。

    image-20241112131807060

  10. 至此也理解了这个移动的公式的妙处，但是如何用代码实现？（利用next数组）

代码思路总结：

  1. 获得子串的部分匹配值表next
  2. 使用部分匹配值表完成kmp搜索

代码实现

KMP

ps：核心的就是两个方法——kmpNext求出子串的部分匹配表，kmpSearchkmp搜索。其中最最核心的，分别是这两个方法中的while语句，是如何处理j的更新的！两个方法中的i和j含义各有不同。至于为什么j = next[j-1]，则见博客底层原理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
package com.yukinoshita.algorithm.kmp;

import java.util.Arrays;

public class KMP {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";

        int[] next = kmpNext(str2);

        System.out.println("部分匹配值表："+Arrays.toString(next));
        System.out.println("匹配的第一个下标为："+kmpSearch(str1,str2,next));
    }

    /**
     * kmp搜索算法
     *
     * @param str1 源字符串
     * @param str2 子串
     * @param next 子串对应的部分匹配表
     * @return 返回第一个匹配的位置，否则-1
     */
    public static int kmpSearch(String str1, String str2, int[] next) {
        for (int i = 0, j = 0; i < str1.length(); i++) {
            //需要处理str1.charAt(i)!=str2.charAt(j)的情况，去调整j的大小
            //KMP算法核心点
            while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
                j = next[j - 1];
            }

            if (str1.charAt(i) == str2.charAt(j)) {
                j++;
            }
            if (j == str2.length()) {
                return i - j + 1;
            }
        }
        return -1;
    }

    //获取子串的部分匹配表
    public static int[] kmpNext(String str) {
        int[] next = new int[str.length()];
        next[0] = 0;//如果字符串长度为1，部分匹配值一定是0

        for (int i = 1, j = 0; i < next.length; i++) {
            //当str.charAt(i) != str.charAt(j)时，需要从next[j-1]获取新的j
            //直到我们发现有 str.charAt(i) == str.charAt(j) 成立时才退出
            //这是kmp算法的核心……
            while (j > 0 && str.charAt(i) != str.charAt(j)) {
                j = next[j - 1];
            }

            //当str.charAt(i) == str.charAt(j)时，部分匹配值就是+1
            if (str.charAt(i) == str.charAt(j)) {
                j++;
            }
            next[i] = j;
        }
        return next;
    }
}