图

为什幺要有图？

  1. 线性表局限于一个直接前驱和一个直接后继。
  2. 树也只能有一个直接前驱。
  3. 当我们需要多对多的关系时，就需要使用图。

图的常用概念

  1. 顶点（vertex）

  2. 边（edge）

  3. 路径

  4. 无向图

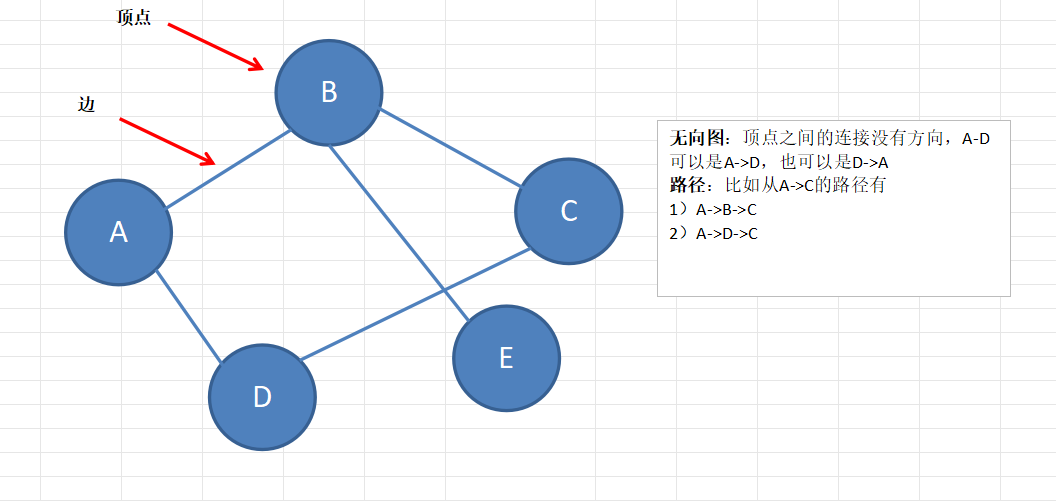
    image-20241110210336286

  5. 有向图

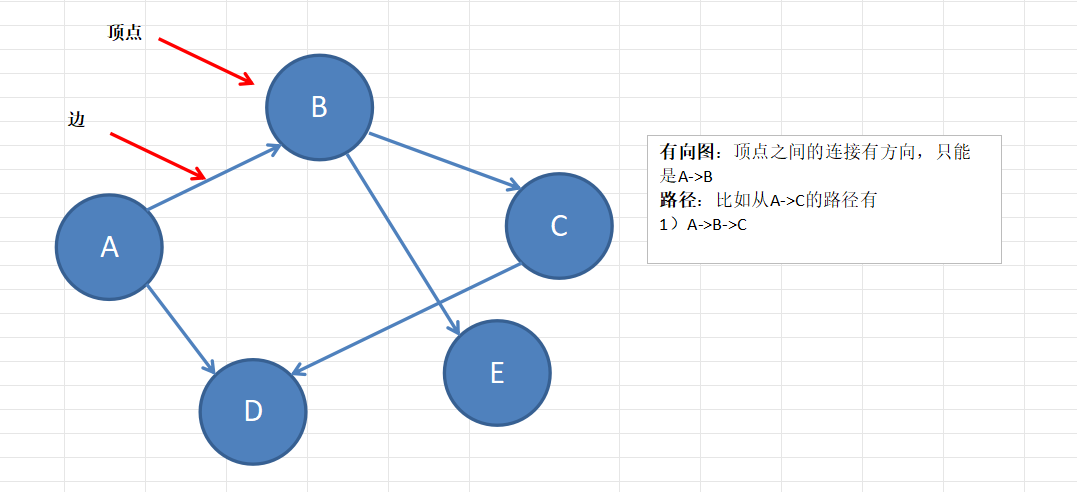
    image-20241110210634499

  6. 带权图（这种边带权值的图也叫网）

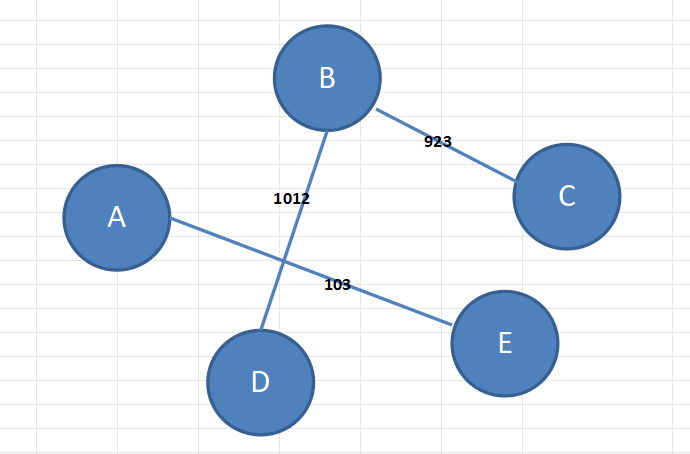
    image-20241110210837126

图的表示方式：二维数组表示（邻接矩阵）；链表表示（邻接表）

  1. 邻接矩阵

    • 邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是的row和col表示的是1…n个点。
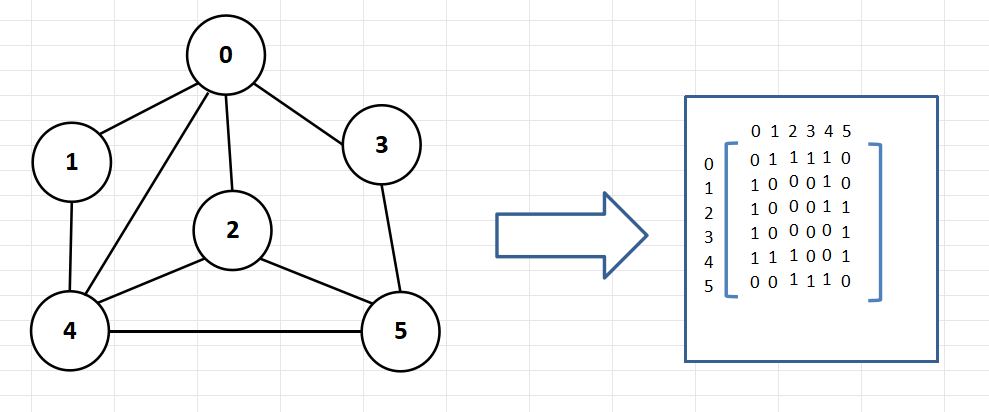
    image-20241113213029646

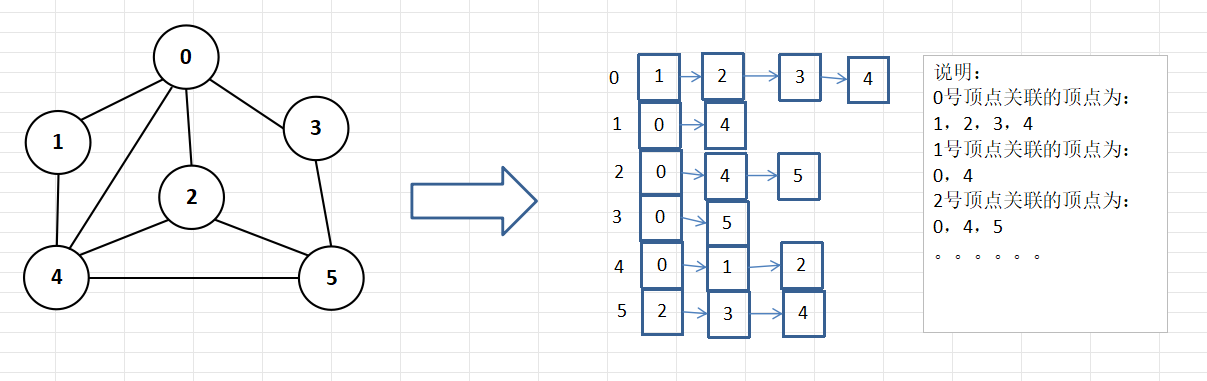
  2. 邻接表

    • 邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在,会造成空间的一定损失。
    • 邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成
    image-20241114115322312

创建一个无向图-简单案例

Graph

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
package com.yukinoshita.dataStructure.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;

public class Graph {

    private ArrayList<String> vertexList;
    private int[][] edges;
    private int numOfEdges; 

    public static void main(String[] args) {
        
        int n = 5;
        String Vertexs[] = {"A", "B", "C", "D", "E"};
        Graph graph = new Graph(n);
        for(String vertex: Vertexs) {
            graph.insertVertex(vertex);
        }
        //添加边
        //A-B A-C B-C B-D B-E
        graph.insertEdge(0, 1, 1); // A-B
        graph.insertEdge(0, 2, 1); //
        graph.insertEdge(1, 2, 1); //
        graph.insertEdge(1, 3, 1); //
        graph.insertEdge(1, 4, 1); //
        graph.showGraph();
    }

    //构造器
    public Graph(int n) {
        edges = new int[n][n];
        vertexList = new ArrayList<String>(n);
        numOfEdges = 0;

    }

    //获取顶点数量
    public int getNumOfVertex() {
        return vertexList.size();
    }
    //展示图
    public void showGraph() {
        for(int[] link : edges) {
            System.err.println(Arrays.toString(link));
        }
    }
    //获取边的数量
    public int getNumOfEdges() {
        return numOfEdges;
    }
    //获取顶点的值
    public String getValueByIndex(int i) {
        return vertexList.get(i);
    }
    //获取权值
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }
    //插入顶点
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }
    //插入边
    public void insertEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }
}