数据结构与算法
数据结构
前言:数据结构,好比是一类基本工具,每一类数据结构被抽象出来,必定有其用途。用好数据结构,就相当于用好了这类基本工具。——工欲善其事必先利其器。
- TODO:数学渲染有问题……后续改一下
算法
排序算法-概论
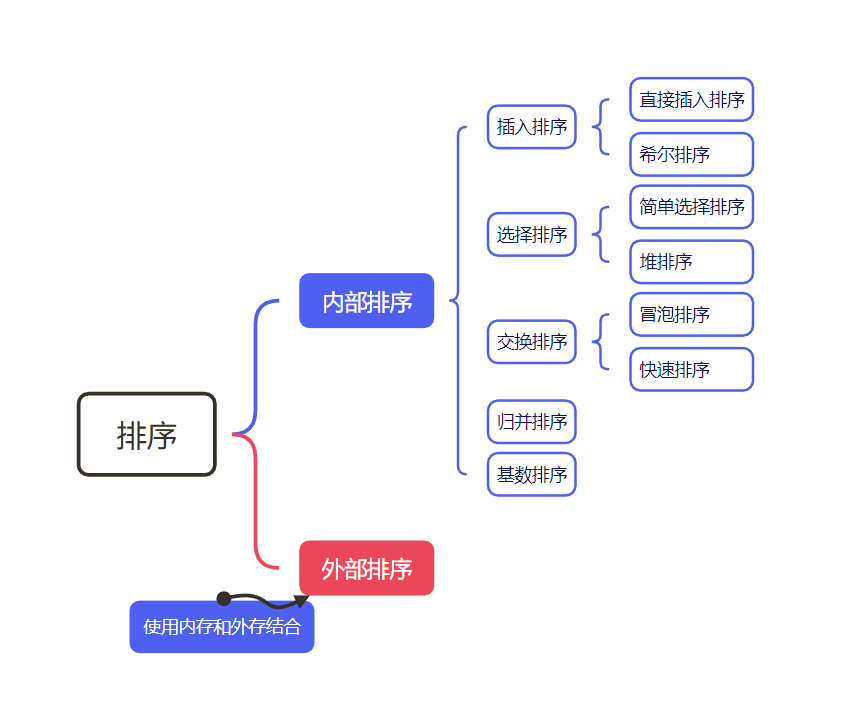
分类
分为内部排序和外部排序,
- 内部排序,是指将要处理的数据都加载到内部存储器(内存)完成排序
- 外部排序,当数据量过大,无法全部加载到内存中时,需要借助外部存储进行排序
算法对比
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | In-place | 稳定 |
| 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | In-place | 不稳定 |
| 插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | In-place | 稳定 |
| 希尔排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n\log^2 n)$ | $O(1)$ | In-place | 不稳定 |
| 归并排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(n)$ | Out-place | 稳定 |
| 快速排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n^2)$ | $O(\log n)$ | In-place | 不稳定 |
| 堆排序 | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(1)$ | In-place | 不稳定 |
| 计数排序 | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | $O(k)$ | Out-place | 稳定 |
| 桶排序 | $O(n+k)$ | $O(n+k)$ | $O(n^2)$ | $O(n+k)$ | Out-place | 稳定 |
| 基数排序 | $O(n \times k)$ | $O(n \times k)$ | $O(n \times k)$ | $O(n+k)$ | Out-place | 稳定 |
术语解释:
- 稳定:如果a原本在b前面,而a=b,排序后a仍在b前面
- 不稳定:如果a原本在b前面,而a=b,排序后a有可能在b后面
- 内排序:所有排序操作都在内存中完成
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行
- 时间复杂度: 一个算法执行所耗费的时间
- 空间复杂度:运行完一个程序所需内存的大小
- n:数据规模
- k:计数排序、桶排序等中桶的数量;基数排序中,数字的位数
- In-place:不占用额外内存
- Out-place:占用额外内存
实际测试的性能
不同算法对于不同测试数据大小的排序所用时间
| 数据量 | 冒泡排序) | 选择排序) | 插入排序) | 希尔排序) | 快速排序) | 归并排序) | 基数排序) | 堆排序) |
|---|---|---|---|---|---|---|---|---|
| 10000 | 43 | 26 | 22 | 3 | 1 | 2 | 2 | 1 |
| 50000 | 1845 | 592 | 431 | 6 | 6 | 7 | 3 | 5 |
| 80000 | 5250 | 1470 | 1074 | 12 | 9 | 18 | 10 | 8 |
| 140000 | 18690 | 4337 | 3214 | 17 | 12 | 22 | 14 | 13 |
| 500000 | 52 | 37 | 57 | 35 | 46 | |||
| 900000 | 104 | 64 | 93 | 35 | 83 |
查找算法-概论
分类
- 顺序(线性)查找
- 二分查找/折半查找
- 插值查找
- 斐波那契查找
简单介绍
- 顺序查找操作的数据可以是无序的(就是遍历……)
- 二分查找、插值查找、斐波那契查找要求在一个有序数组中
中缀表达式
中缀表达式,就是我们常见的表达式,如$(3+4) \times 5-6$,但是对于计算机来说操作较为复杂。
因此,在计算结果时,一般需要转换为其他表达式来计算(一般是后缀表达式)
前缀表达式
前缀表达式,又称波兰式。前缀表达式的运算符位于操作数之前
e.g.$(3+4)\times5-6$对应的前缀表达式为$-*+3456$ (关键在于将原先表达式转换为前缀表达式)
- 前缀表达式的求值:
- 从右至左扫描前缀表达式,遇到数字时,压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对他们进行运算,并将结果入栈。重复该过程直至表达式最左端。
- e.g. $-*+3456$
- 将6、5、4、3压入堆栈(
numStack=[6,5,4,3]) - 遇到+,弹出3、4,运算$3+4=7$,将7入栈。(
numStack=[6,5,7]) - 遇到*,弹出7、5,运算$7 \times 5=35$,将35入栈(
numStack=[6,35]) - 遇到-,弹出35、6,运算$35-6=29$,将29入栈(
numStack=[29])
后缀表达式
后缀表达式,又称逆波兰表达式,与前缀表达式类似,只是运算符放在操作数之后。
例如$(3+4)\times 5 -6$的后缀式为:$3 \quad 4 + 5 \times 6 - $
$a+b$为$a \quad b +$
- $a+(b-c)$为$a \quad b \quad c - +$
- $a+(b-c)\times d$为$a \quad b \quad c - d \times +$
- $a+d \times (b-c)$为$a \quad d \quad b \quad c - \times +$
- $a=1+3$为$a \quad 1 \quad 3 +=$
后缀表达式的求值:
从左至右表达式,遇到数字时,压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对他们进行运算,并将结果入栈。重复该过程直至表达式最右端。(演示过程和前缀表达式一致)
关键在于如何将中缀表达式转换为后缀表达式
递归
递归介绍
简单来说,递归就是自己调用自己,每次调用时传入不同的变量。
递归调用机制:
- 当程序每次调用一个方法时,就会开辟一个独立的空间(栈)
- 每个空间的数据(局部变量),都是独立的
递归能解决的问题:
- 数学类:八皇后问题、汉诺塔、阶乘问题、迷宫问题、球和篮子问题
- 算法中:快排、归并排序、二分查找、分治算法
- 将用栈解决的问题->使用递归,代码简洁
递归需遵守的规则
- 执行一个方法,就创建一个独立空间
- 局部变量独立
- 引用类型变量是共享的(例如数组)
- 递归必须设计递归出口,必须向退出递归的条件逼近
- 当一个方法执行完毕,谁调用,谁接收返回结果,并且继续执行调用者后面的代码
分治
- 分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)……
- 分治算法可以求解的一些经典问题
- 二分搜索
- 大整数乘法
- 棋盘覆盖
- 合并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
分治算法的基本步骤
分治法在每一层递归上都有三个步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
- 合并:将各个子问题的解合并为原问题的解。
分治(Divide-and-Conquer(P))算法设计模式:
1 | if |P|≤n0 |
其中$|P|$表示问题P的规模;$n_0$为一阈值,表示当问题P的规模不超过$n_0$时,问题已容易直接解出,不必再继续分解。ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过$n_0$时直接用算法ADHOC(P)求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。
基数排序处理负数
偏移法
介绍
- 找出最小值:首先遍历数组,找出最小值。
- 偏移所有数:将数组中的所有元素都加上一个正数,使得数组中的所有元素都变为非负数。这个正数可以是绝对值最小值加一。例如,如果最小值是 -10,可以将所有元素加 11,使得最小值变为 1。
- 进行基数排序:对偏移后的数组进行基数排序。
- 恢复原值:排序完成后,再将每个元素减去之前加的正数,恢复到原始值。
代码实现
1 | private static void radixSort(int[] arr) { |
解释
- 偏移处理:在进行排序前,将所有数加上偏移量(绝对值最小值),确保数组中所有元素为非负数。
- 基数排序:对偏移后的数组进行基数排序。
- 恢复值:排序完成后,减去偏移量以恢复到原始值。
这种方法较为简单,且在排序完成后,时间复杂度仍然保持在 $(O(d \cdot (n + k)))$,其中 d 是数字的位数,n 是元素个数,k 是基数的大小。
分开处理
介绍
- 分为正负数组:创建两个数组,分别存放正数和负数。
- 对正数进行基数排序:对正数数组进行基数排序。
- 对负数进行基数排序:对负数数组的绝对值进行基数排序,然后将结果反转。
- 合并结果:将负数数组(排序后)和正数数组(排序后)合并。
代码实现
1 | import java.util.Arrays; |
解释
分开处理:
- 使用
Arrays.stream分别创建正数数组positive和负数数组negative(取绝对值)。
- 使用
基数排序:
- 对正数数组调用
radixSortPositive方法进行排序。 - 对负数数组同样调用
radixSortPositive,但处理时将元素取绝对值。
- 对正数数组调用
反转负数数组:
- 对负数排序后的结果进行反转,以确保负数按正确顺序排列。
合并结果:
- 先将负数(带负号)放入最终数组,再将正数放入,得到完整的排序结果。
两者比较、总结
偏移法
优点:
- 实现相对简单,不需要额外的空间来存储正数和负数数组。
- 对于负数和正数的排序都是在同一个数组中进行的,合并结果的步骤被省略。
缺点:
- 需要对整个数组进行遍历以找出最小值并计算偏移量,这在数据量很大时会增加时间开销。
- 需要额外的空间用于桶(假设桶大小为常数,空间复杂度为 $O(n)$),但实际上,空间利用率可能受到偏移量影响。
分开处理法
优点:
- 明确分开了负数和正数的排序,逻辑更清晰。
- 在处理负数时,直接对绝对值排序,可以有效避免负数带来的问题。
缺点:
- 需要额外的数组来存储正数和负数,空间复杂度更高(需要 $O(n)$ 的额外空间)。
- 合并结果时需要再次遍历数组,增加了额外的时间开销。
性能比较
- 时间复杂度:两种方法的时间复杂度均为 $O(d \cdot (n + k))$,其中 $d$ 是数字的位数,$n$ 是元素个数,$k$ 是基数的大小。因此,从理论上讲,时间复杂度相同。
- 实际性能:
- 对于大多数情况,偏移法在空间上更高效,适合数据范围较小的情况。
- 分开处理法在逻辑上更易于理解,且能更好地处理极端情况(例如全是负数或全是正数)。
结论
在性能上,两种方法在大多数情况下相似,但具体的选择可以根据实际需求和数据特性来决定。
如果需要处理的数组范围较大且包含负数,分开处理法可能会更加灵活;如果希望简化实现,偏移法是一个不错的选择。
斐波那契查找的意义何在?
这个问题,我浅浅看了几篇文章,但都没有满意的答案。
可能的原因千奇百怪:
- 斐波那契查找在计算
mid值时,只使用了加减法——mid = low + f[k-1] - 1,而二分查找使用了除法,除法是极耗费时间的。但是吧,也没那么耗时间,很多编辑器都优化成>>1了,也没比加减法慢。 - 斐波那契查找将mid点设置在0.618处,如果所以元素落在$[low,mid-1]$区间的概率较大,判断一次的可能更高;而二分查找两个区间长度都为一半,所以仅需判断一次的概率相比更小。貌似很有道理,但是为什么是0.618?我没看到一篇文章有过详细的数学证明……所以还是觉得这两者查找效率半斤八两。
自用の界面菜单
1 | char operate = ' '; |
前缀编码
简单理解:10010110100是编码结果,但是在解读时,a编码为1,b编码为10,那么在解读这个编码时,开头的1究竟是1?还是说10是b?
如果在一个编码方案中,任何一个编码都不是其他任何编码的前缀(最左子串),则称该编码是前缀编码。
动态规划
动态规划介绍:
- 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
- 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
- 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
- 动态规划可以通过填表的方式来逐步推进,得到最优解
贪心算法
贪心算法介绍:
- 贪婪算法(贪心算法)是指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法
- 贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果








