Manacher算法

该算法用于解决“最长回文子串”的问题

例题：5. 最长回文子串

暴力来解题的话，一般时间复杂度是$O(n^2)$，使用中心扩展法或者二维动态规划

而Manacher算法能$以O(n)$的时间复杂度来解决这个问题。

以下撰写内容参考自灵神b站视频讲解，感谢灵神！

为什么Manacher算法有这种魔力呢？关键在于它能**$O(1)$地判断任意子串是否回文**

比如：

image-20251101235035918

说明：每个字母下方数字表示以该字母为中心，所能得到的最长回文子串的长度，假设目前已经拿到了这些值，那么如何$O(1)$地向下判断剩余的字母（以他们为中心）呢？

比如如下红色框选了c b a b c ，那么这个子串的中心就是a，而a的长度是11（蓝色框），显然这个红色框是在蓝色框之内的，要是依次把红色框之外、蓝色框之内的d、a、b去掉，得到的c b a b c显然是回文的。

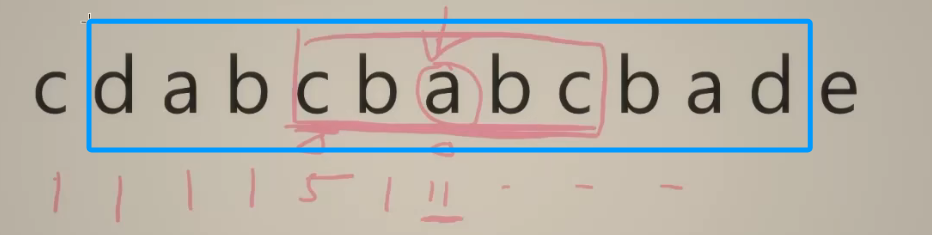
image-20251101235614429

又如下，要求右边c的最长回文子串长度，怎么利用之前已经求过的信息呢？

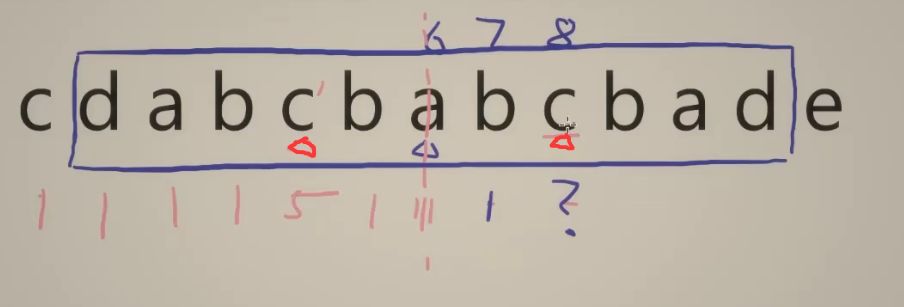
image-20251102000040924

重点：想象有一面镜子，以a为中心，那么下标为8位置的c的镜像位置的c’就是下标为5的这个。下标为5的这个c’的最长回文子串长度我们是知道的，是5，而这个长度对于下标位置为8的c来说没有超出蓝色盒子的右边界，所以以下标8位置为中心的最长回文子串长度就是5，省去了暴力做法（以它为中心，然后左右指针不断扩展……现在不需要了）。这就是算法的核心思想。

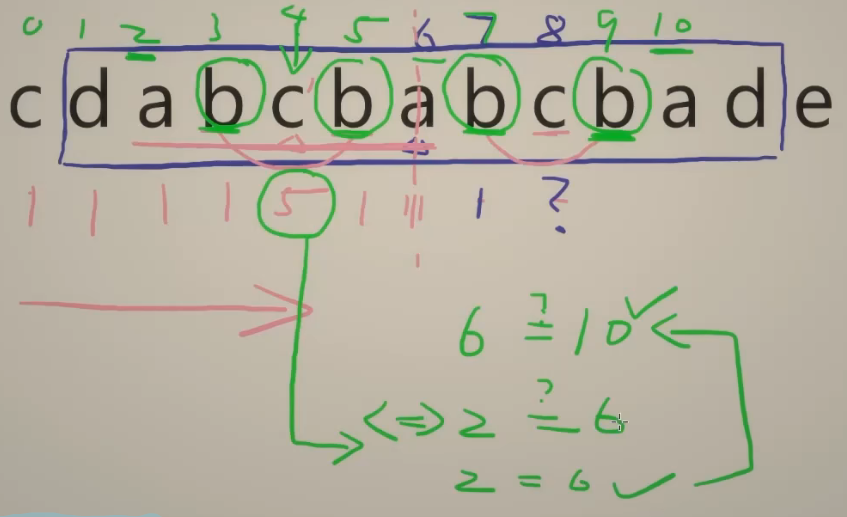
image-20251102111654126

对于下标为8的c，要比较7和9是否相同，等价于比较3和5是否相同；要比较6和10是否相同，等价于比较2和6是否相同。但是7和9，6和10都不需要比较，因为8的镜像位置是4，而4已经告诉我们了。

但是如果出界（出了蓝色盒子右边界boxR）

这里贴出对应这一思想的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for(int i=2;i<halfLen.length;i++){
    int hl = 1;
    if(i < boxR){
        //这个if语句就是关键代码（删去后就变成O(n^2)复杂度）
        hl = Math.min(halfLen[boxM*2-i],boxR-i);
    }

    //暴力扩展
    while(t[i-hl] == t[i+hl]){
        hl++;
        boxM = i;
        boxR = i+hl;
    }

    halfLen[i] = hl;
    if(hl > halfLen[maxI]){
        maxI = i;
    }
}

为了实现算法，还有其他问题要解决，那就是偶数串的回文中心怎么办？总不能夹在两个字母中间。也有比较好的方法：

那就是原先的字符串s每两个中间插入一个’#‘转变为新字符串t，但是前后都要加’#'且最前和最后还要加入两个不同的字符（用于防止下标出界）

image-20251102113020080

最左边加’^‘最右边加’$‘是因为这两个字符与其他字符均不同，所以在进行扩展时while(s[i]==s[j])判断时，肯定不会使得i或者j出界。起到了哨兵的作用。而中间’#‘的插入，使得当’#'作为子串中心点时，相当于原字符串是以偶字符串在进行扩展；当以字母为中心点时，相当于原字符串是以奇字符串在进行扩展。

image-20251102113544263

定义halfLen[i]：例如c下面的5，代表的是扩展后的字符串t，以c为中心点时，最长回文子串的长度的一半（包括c自身）

那么原字符串s和新字符串t的对应关系呢？试着举个简单例子推导一下：

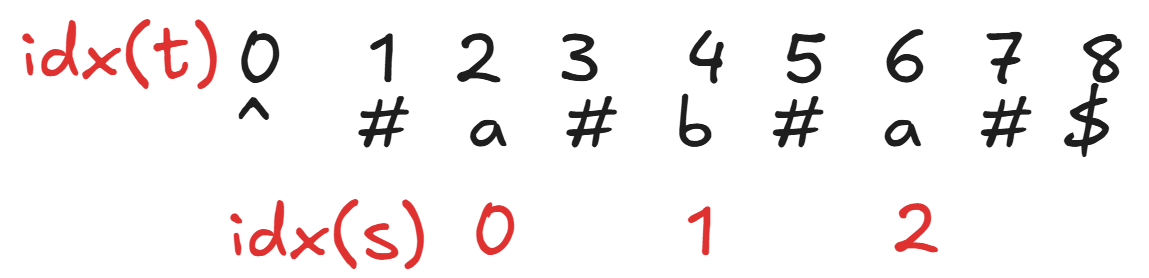
image-20251102115008245

所以有公式$i_t = 2*i_s + 2$。故$i_s = \frac{i_t-2}{2}$

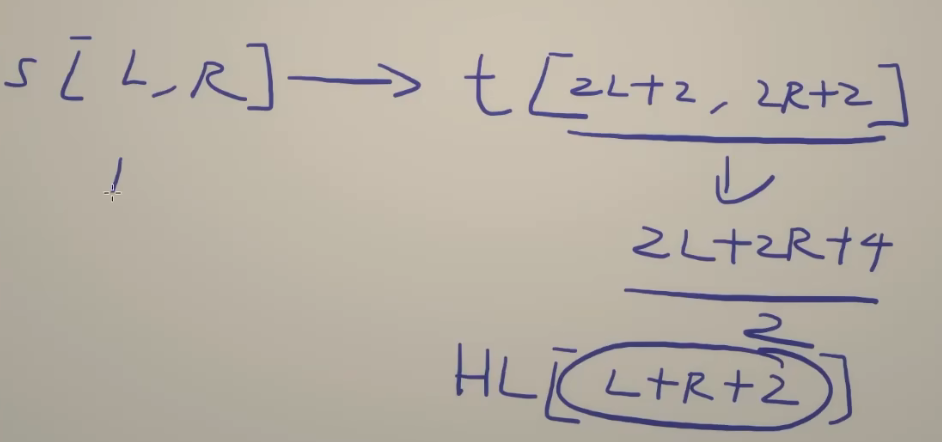
image-20251102115326582

解释：当我们要判断$s[L,R]$区间是否为回文串时，对应的就是判断$t[2L+2,2R+2]$区间是否是回文串，那么t的这个区间的中心点就是$\frac{2L+2R+4}{2}=L+r+2$，因此只需要看$halfLen[L+R+2]$的值就可以了。

剩下的需要仔细看代码怎么写的，懂了大体思路看代码会容易些：

下面直接使用灵神代码

作者：灵茶山艾府
链接：https://leetcode.cn/problems/longest-palindromic-substring/solutions/2958179/mo-ban-on-manacher-suan-fa-pythonjavacgo-t6cx/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
    public String longestPalindrome(String s) {
        // Manacher 模板
        // 将 s 改造为 t，这样就不需要讨论 len(s) 的奇偶性，因为新串 t 的每个回文子串都是奇回文串（都有回文中心）
        // s 和 t 的下标转换关系：
        // (si+1)*2 = ti
        // ti/2-1 = si
        // ti 为偶数，对应奇回文串（从 2 开始）
        // ti 为奇数，对应偶回文串（从 3 开始）
        int n = s.length();
        char[] t = new char[n * 2 + 3];
        Arrays.fill(t, '#');
        t[0] = '^';
        for (int i = 0; i < n; i++) {
            t[i * 2 + 2] = s.charAt(i);
        }
        t[n * 2 + 2] = '$';

        // 定义一个奇回文串的回文半径=(长度+1)/2，即保留回文中心，去掉一侧后的剩余字符串的长度
        // halfLen[i] 表示在 t 上的以 t[i] 为回文中心的最长回文子串的回文半径
        // 即 [i-halfLen[i]+1,i+halfLen[i]-1] 是 t 上的一个回文子串
        int[] halfLen = new int[t.length - 2];
        halfLen[1] = 1;

        // maxI 记录最长回文子串在 halfLen 中的下标
        int maxI = 0;
        // boxR 表示当前右边界下标最大的回文子串的右边界下标+1
        // boxM 为该回文子串的中心位置，二者的关系为 r=mid+halfLen[mid]
        int boxM = 0;
        int boxR = 0;
        for (int i = 2; i < halfLen.length; i++) {
            int hl = 1;
            if (i < boxR) {
                // 记 i 关于 boxM 的对称位置 i'=boxM*2-i
                // 若以 i' 为中心的最长回文子串范围超出了以 boxM 为中心的回文串的范围（即 i+halfLen[i'] >= boxR）
                // 则 halfLen[i] 应先初始化为已知的回文半径 boxR-i，然后再继续暴力匹配
                // 否则 halfLen[i] 与 halfLen[i'] 相等
                hl = Math.min(halfLen[boxM * 2 - i], boxR - i);
            }

            // 暴力扩展
            while (t[i - hl] == t[i + hl]) {
                hl++;
                boxM = i;
                boxR = i + hl;
            }

            halfLen[i] = hl;
            if (hl > halfLen[maxI]) {
                maxI = i;
            }
        }

        int hl = halfLen[maxI];
        // 注意 t 上的最长回文子串的最左边和最右边都是 '#'
        // 所以要对应到 s，最长回文子串的下标是从 (maxI-hl)/2 到 (maxI+hl)/2-2
        return s.substring((maxI - hl) / 2, (maxI + hl) / 2 - 1);
    }
}