斐波那契查找算法（黄金分割法）

思路分析

基本介绍：

  1. 黄金分割点是指将一条线段分成两段，使其中一部分与全长的比例等于另一部分与这部分之比，近似值$0.618$。
  2. 斐波那契数列${1,1,2,3,5,8,13,21,34,55}$，发现斐波那契数列两个相邻数的比例无限接近于黄金分割0.618。
    • ps：$fibo[n]=fibo[n-1]+fibo[n-2],n>2;fibo[1]=fibo[2]=1$

原理：

斐波那契查找和二分查找、插值查找很像，仅仅改变了中间结点mid，即$mid = low+F(k-1)-1$

对于$F(k-1)-1$的理解：(结合图进行理解！)

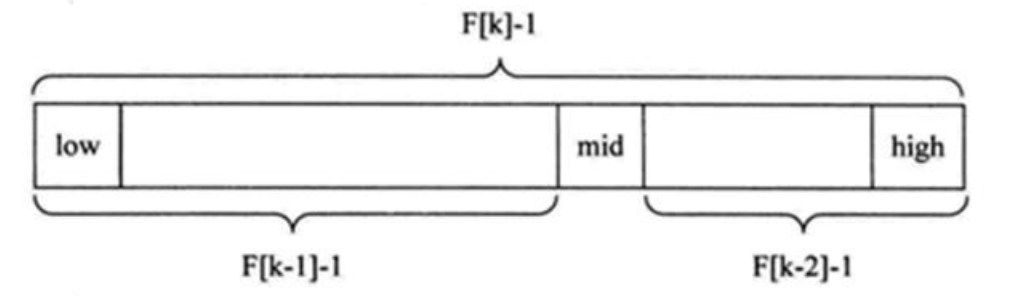
image-20241102174615812

  1. 由斐波那契数列$F[k]=F[k-1]+F[k-2]$的性质，可以得到$(F[k]-1) = (F[k-1]-1)+(F[k-2]-1)+1$，这里把每一个括号看成一个整体，对应上图的三个部分！可见等式右边的+1就是mid。即：mid = low + F(k-1)-1

  2. 类似的，每一个子段也可以照此方式进行分割

  3. 但顺序表长度n不一定刚好等于$F[k]-1$，所以需要将原来的顺序表长度n增加至$F[k]-1$。这里的k值只要能使得$F[k]-1$大于等于n即可，由while(n>fib(k)-1) k++得到k值。顺序表长度增加后，新增的位置n+1到fib[k]-1都赋值为n位置的值即可。

第三点相对不好理解，结合代码来看吧。

代码实现

代码实现一定要多看多理解，不是那种光看理论就能立刻想出来对应代码的算法

FibonacciSearch

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
package com.yukinoshita.algorithm.search;

import java.util.Arrays;

public class FibonacciSearch {

    public static int maxSize = 20;

    public static void main(String[] args) {
        int[] arr = {1, 8, 10, 89, 520, 1000, 1234,};
        System.out.println("index = "+fibSearch(arr,89));
    }

    //非递归方式得到一个fibonacci数列数组
    public static int[] fib() {
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }

    /**
     * 斐波那契查找算法
     * 使用非递归方式编写
     *
     * @param arr 数组
     * @param key 需要查找的关键码
     * @return 返回对应的下标，没有则返回1
     */
    public static int fibSearch(int[] arr, int key) {
        int low = 0;
        int high = arr.length - 1;
        int k = 0;//表示斐波那契分割数值的下标
        int mid = 0;
        int[] f = fib();
        //获取到k值
        while (high > f[k] - 1) {
            k++;
        }
        //因为f[k]的值可能大于arr的长度，因此使用Arrays类，构造一个新的数组，指向arr[]
        //不足的部分用0补足
        int[] temp = Arrays.copyOf(arr, f[k]);
        //新填充的部分用原数组的最后一个元素补齐
        for (int i = high + 1; i < arr.length; i++) {
            temp[i] = arr[high];
        }

        while (low <= high) {
            mid = low + f[k - 1] - 1;
            if(key < temp[mid]) { // 说明应该继续向左边查找
                high = mid - 1;
                //k--的说明：
                //全部元素 = 前面元素 + 后面元素
                //f[k] = f[k-1] + f[k-2]
                //因为前面有f[k-1]个元素
                //所以k--，相当于下次是对前面的、大小为f[k-1]的数组操作
                k--;
            }else if(key > temp[mid]) {
                low = mid + 1;
                //k -=2的说明：
                //全部元素 = 前面元素 + 后面元素
                //f[k] = f[k-1] + f[k-2]
                //因为后面有f[k-2]个元素
                //所以k-=2，相当于下次是对后面的、大小为f[k-2]的数组操作
                k -=2;
            }else{//找到
                //但需要确定返回的是哪个
                if(mid<=high){
                    return mid;
                }else{
                    return high;
                }
            }
        }
        return -1;
    }
}