Floyd算法

Floyd算法介绍

  1. 和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名
  2. 弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
  3. 迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径
  4. 弗洛伊德算法 VS 迪杰斯特拉算法：迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径；弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径。

弗洛伊德算法思路：

  1. 假设图中有顶点 $ v_i $、$ v_j$ 和 $ v_k $，其中 $ L_{ik} $表示从顶点 $v_i $到顶点 $ v_k $ 的最短路径，$ L_{kj} $ 表示从顶点 $ v_k $ 到顶点 $ v_j $ 的最短路径。那么，顶点 $ v_i $ 到顶点 $ v_j $ 的最短路径 $ L_{ij} $ 可以通过以下方式计算：

$$
L_{ij} = \min(L_{ij}, L_{ik} + L_{kj})
$$

也就是说，从 $ v_i $ 到 $ v_j $ 的最短路径，可能是直接从 $ v_i $ 到 $ v_j $ 的路径（即 $ L_{ij} $），或者是通过一个中间顶点 $ v_k $ 经过 $ v_k $ 的路径，即先从 $ v_i $ 到 $ v_k $，再从 $ v_k $ 到 $ v_j $。

  1. 在实际算法中，针对每一对顶点 $ (v_i, v_j) $，我们都会依次考虑所有可能的中间顶点 $ v_k $（即图中的每个顶点），计算并更新从 $ v_i $ 到 $ v_j $ 的最短路径。具体来说，对于每一个中间顶点 $ v_k $，我们更新所有顶点对 $ (v_i, v_j) $ 的最短路径：

    $$
    L_{ij} = \min(L_{ij}, L_{ik} + L_{kj})
    $$

  2. 最终，当所有的顶点都作为中间点被考虑过之后，我们就能够得到每一对顶点之间的最短路径。

图解：

求每A-G点到其余各点的最短路径/距离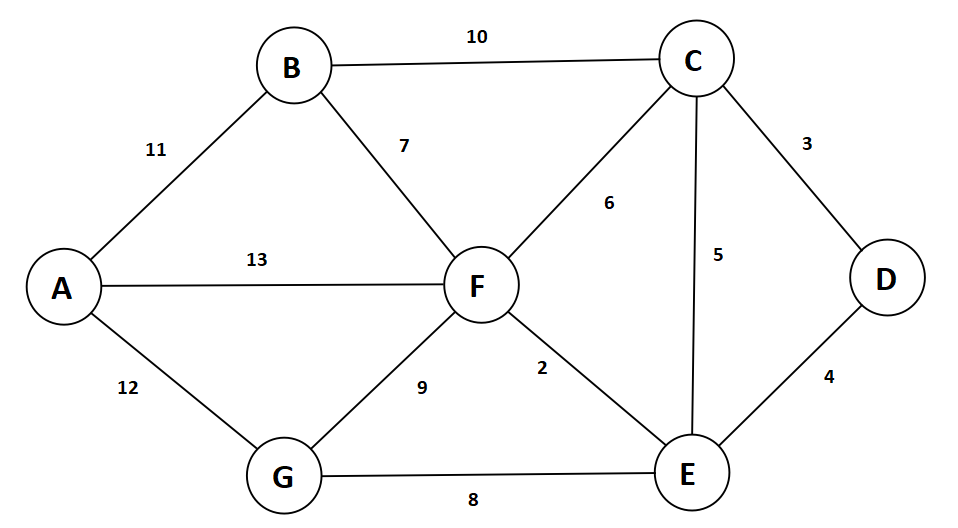？image-20241114144607382

  1. 在算法进行过程中，重点维护两张表：距离表、前驱表，初始化如下：

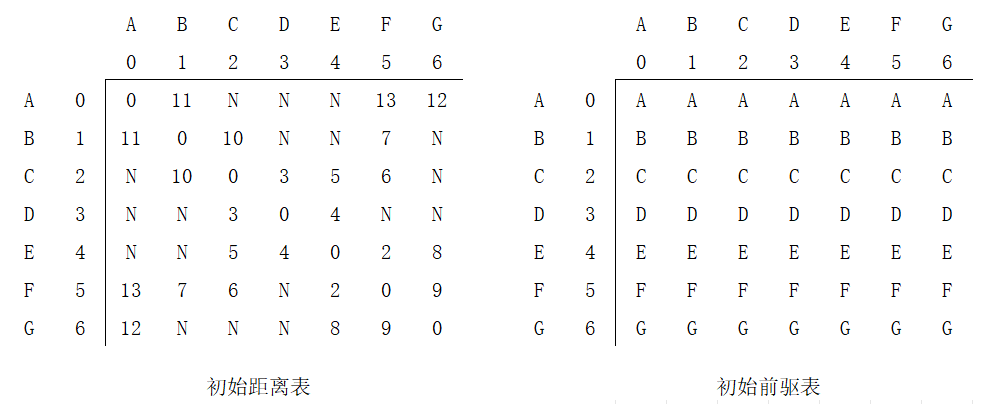
    image-20241114145839072

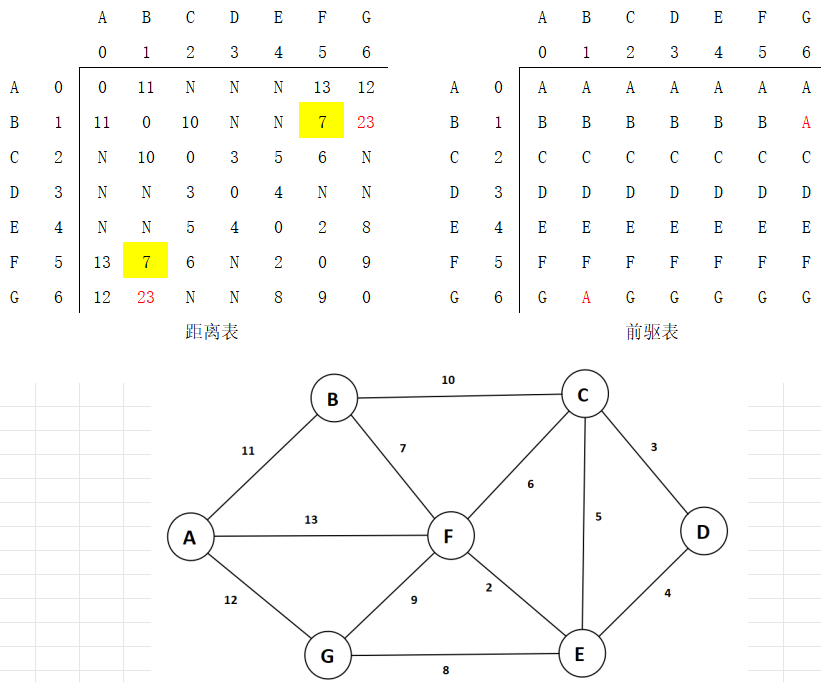
  2. 仅以第一次为例，将A作为中间节点，对两张表进行更新：其中，只更新了B-A-G[23]（经过中间顶点A），故更新B-G为23，标黄的B-F[7]比B-A-F[24]小，所以不更新B-F。

    image-20241114150317574

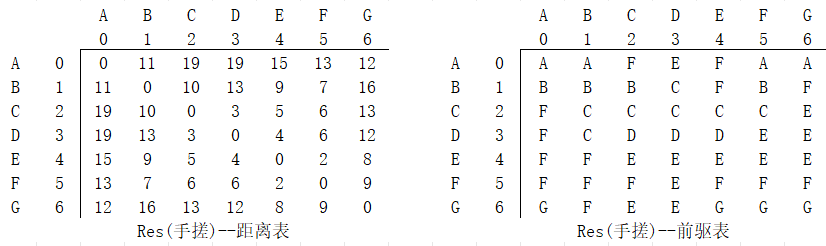
  3. 真–人工手动跑一遍结果（代码验证无误）

    image-20241114154612640

代码实现

FloydAlgorithm

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
package com.yukinoshita.algorithm.floyd;

import java.util.Arrays;

public class FloydAlgorithm {
    public static final int N = 65535;
    public static void main(String[] args) {
        char[] vertex = {'A','B','C','D','E','F','G'};
        int[][] matrix = {
                {0, 11, N, N, N, 13, 12},
                {11, 0, 10, N, N, 7, N},
                {N, 10, 0, 3, 5, 6, N},
                {N, N, 3, 0, 4, N, N},
                {N, N, 5, 4, 0, 2, 8},
                {13, 7, 6, N, 2, 0, 9},
                {12, N, N, N, 8, 9, 0}
        };
        Graph graph = new Graph(vertex.length,vertex,matrix);
        graph.floyd();
        graph.showGraph();

        System.out.print("输出某两点的最短路径:");
        graph.path(0,3);//输出A到D的最短路径
    }
}

class Graph {
    private char[] vertex;
    private int[][] dis;//最短路矩阵
    private int[][] pre;//前驱矩阵

    public Graph(int n, char[] vertex, int[][] matrix) {
        this.vertex = new char[n];
        this.dis = new int[n][n];
        this.pre = new int[n][n];
        //初始化
        for (int i = 0; i < n; i++) {
            this.vertex[i] = vertex[i];
            for (int j = 0; j < n; j++) {
                dis[i][j] = matrix[i][j];
                pre[i][j] = i;
            }
        }
    }

    public void showGraph(){
        System.out.println("距离表为：");
        for(int i =0;i<dis.length;i++){
            System.out.println(Arrays.toString(dis[i]));
        }
        System.out.println("前驱表为：");
        for(int i =0;i<pre.length;i++){
            System.out.println(Arrays.toString(pre[i]));
        }
    }

    public void floyd(){
        int len = 0;
        for(int k =0;k<dis.length;k++){//遍历中间节点
            //从i到j  与  从i到k再到j的比较。
            for(int i =0;i<dis.length;i++){
                for(int j =0;j<dis.length;j++){
                    len = dis[i][k] + dis[k][j];
                    if(len < dis[i][j]){
                        dis[i][j] = len;
                        pre[i][j] = pre[k][j];
                    }
                }
            }
        }
    }

    public void path(int v1, int v2) {
        if (v1 == v2) {
            System.out.print(vertex[v1] + " ");
        } else if (pre[v1][v2] == v1) {
            System.out.print(vertex[v1] + " " + vertex[v2] + " ");
        } else {
            path(v1, pre[v1][v2]); // 递归输出路径
            System.out.print(vertex[v2] + " ");
        }
    }


}