1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
| package com.yukinoshita.algorithm.dijkstra;
import java.util.Arrays;
public class DijkstraAlgorithm {
public static void main(String[] args) {
char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
final int N = 65535;
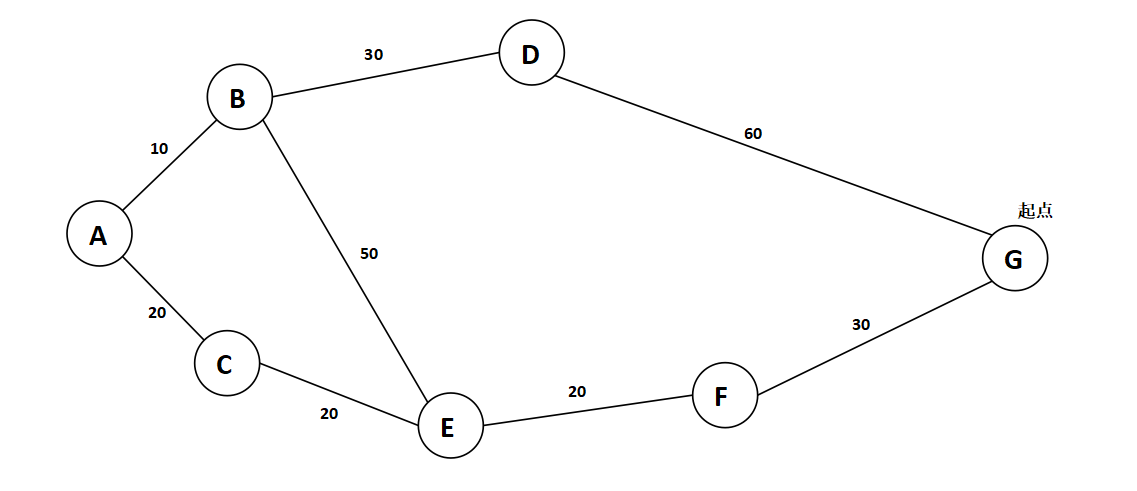
int[][] matrix = {
{0, 10, 20, N, N, N, N},
{10, 0, N, 30, 50, N, N},
{20, N, 0, N, 10, N, N},
{N, 30, N, 0, N, N, 60},
{N, 50, 10, N, 0, 20, N},
{N, N, N, N, 20, 0, 30},
{N, N, N, 60, N, 30, 0}
};
Graph graph = new Graph(vertex, matrix);
graph.dijkstra(6);
graph.showResult();
}
}
class Graph {
private char[] vertex;
private int[][] matrix;
private VisitedVertex vis;
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
public void showGraph() {
for (int[] m : matrix) {
System.out.println(Arrays.toString(m));
}
}
public void dijkstra(int index) {
vis = new VisitedVertex(vertex.length, index);
update(index);
for (int j = 1; j < vertex.length; j++) {
index = vis.updateArr();
update(index);
}
}
private void update(int index) {
int len = 0;
for (int j = 0; j < matrix[index].length; j++) {
len = vis.getDis(index) + matrix[index][j];
if (!vis.isVisited(j) && len < vis.getDis(j)) {
vis.updatePre(j, index);
vis.updateDis(j, len);
}
}
}
public void showResult() {
System.out.println("所有顶点是否都已访问过?visted[]为:"+Arrays.toString(vis.visited));
int start = 0;
for (int i = 0; i < vis.dis.length; i++) {
if (vis.dis[i] == 0) {
start = i;
break;
}
}
System.out.println("起点" + vertex[start] + "到其余顶点的最短距离为:");
for (int i = 0; i < vertex.length; i++) {
System.out.println(vertex[start] + "->" + vertex[i] + "(" + vis.dis[i] + ")");
}
System.out.println("每个顶点的前驱顶点为:");
for (int i = 0; i < vertex.length; i++) {
if (vertex[i] != vertex[vis.preVisited[i]]) {
System.out.println(vertex[i] + "的pre是" + vertex[vis.preVisited[i]]);
} else {
System.out.println(vertex[i] + "是起始点");
}
}
}
}
class VisitedVertex {
public int[] visited;
public int[] preVisited;
public int[] dis;
public VisitedVertex(int vertexNums, int index) {
this.visited = new int[vertexNums];
this.preVisited = new int[vertexNums];
this.dis = new int[vertexNums];
Arrays.fill(dis, 65535);
dis[index] = 0;
visited[index] = 1;
for (int i = 0; i < preVisited.length; i++) {
preVisited[i] = i;
}
}
public boolean isVisited(int index) {
return visited[index] == 1;
}
public void updateDis(int index, int len) {
dis[index] = len;
}
public void updatePre(int pre, int index) {
preVisited[pre] = index;
}
public int getDis(int index) {
return dis[index];
}
public int updateArr() {
int minLen = 65535, index = 0;
for (int i = 0; i < visited.length; i++) {
if (visited[i] == 0 && dis[i] < minLen) {
minLen = dis[i];
index = i;
}
}
visited[index] = 1;
return index;
}
}
|