背包问题

在解决 0-1 背包问题时，我们的目标是选择若干物品放入背包，使得背包内物品的总价值最大，同时遵循背包容量的限制。具体来说，给定一组物品，每个物品都有一个 重量 和 价值，并且背包的容量也是有限的。我们需要从这些物品中选择一些，放入容量有限的背包中，要求背包内物品的 总重量不超过背包的容量，而 总价值最大。

0-1 背包的动态规划解法：

  1. 设有 $n$个物品，每个物品 $i $的 价值 为 $ v[i]$，重量 为 $w[i]$，背包的最大容量为 $C$。
  2. 定义一个二维数组 $ dp[i][j] $，表示考虑前 $ i $ 个物品，背包容量为 $j $ 时，能够获得的最大价值。即$ dp[i][j] $ 是当前背包容量 $j $ 和物品选择方案下的最大价值。

递推公式：

  • 初始化：

    • $dp[0][j] = 0 $（表示没有物品时，背包的最大价值为 0）
    • $dp[i][0] = 0 $（表示背包容量为 0 时，无论选择哪些物品，总价值也为 0）

  • 状态转移：
    对于每个物品 $ i $和每个容量 $j$：

    • 如果当前物品的重量 $w[i] > j$（即当前背包容量不足以容纳这个物品），那么不能放入该物品，此时的最优解就是不放物品 $i$，即：
      $dp[i][j] = dp[i-1][j]$

    • 如果当前物品的重量 $w[i] \leq j$（即背包容量足够容纳当前物品），有两种选择：

      1. 不选择物品 $i $，此时的最优解为 $dp[i-1][j] $（即与不放入该物品时的情况一样）。
      2. 选择物品 $ i $，此时的最优解为物品 $ i $ 的价值加上剩余容量 $j - w[i] $ 能容纳的最大价值，即 $dp[i-1][j - w[i]] + v[i] $。

      这时我们需要取两者中的最大值：
      $$
      dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
      $$

总结：

  • $ dp[i][j] $ 表示在考虑前 $ i $ 个物品、容量为 $ j $ 的背包时，能够获得的最大价值。
  • 对于每个物品 $ i $，如果它的重量 $ w[i] $ 超过当前背包容量 $ j $，就不能选它；否则，我们就要在 选择它 或 不选择它 之间做出最优决策，选择价值更大的方案。

完整算法：

  1. 初始化 $ dp[0][j] = 0 $ 和 $ dp[i][0] = 0 $。
  2. 对每个物品 $ i $ 和每个背包容量 $ j $ 更新 $ dp[i][j] $。
  3. 最终答案就是 $ dp[n][C] $，表示在所有 $ n $ 个物品和容量为 $ C $ 的背包情况下，能够获得的最大价值。

图解

  1. weights物品重量、values物品价值、dp用于求解的数组（初始化如下）（黄色部分是未来求解区）

    image-20241114134226051

  2. 当考虑第一件物品时：

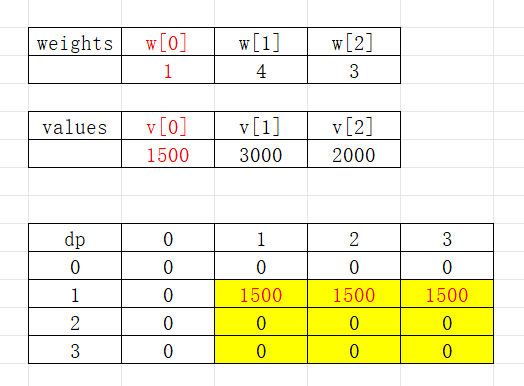
    image-20241114134455411

  3. 考虑第二件物品时：

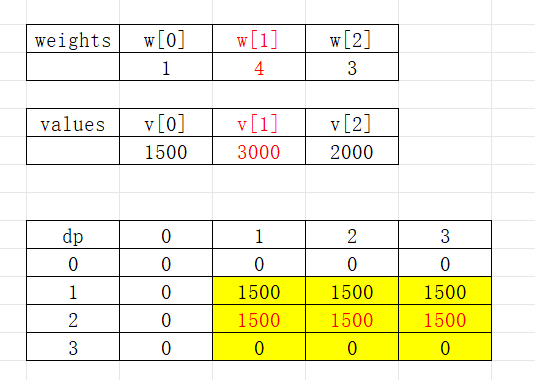
    image-20241114134526878

  4. 考虑第三件物品：

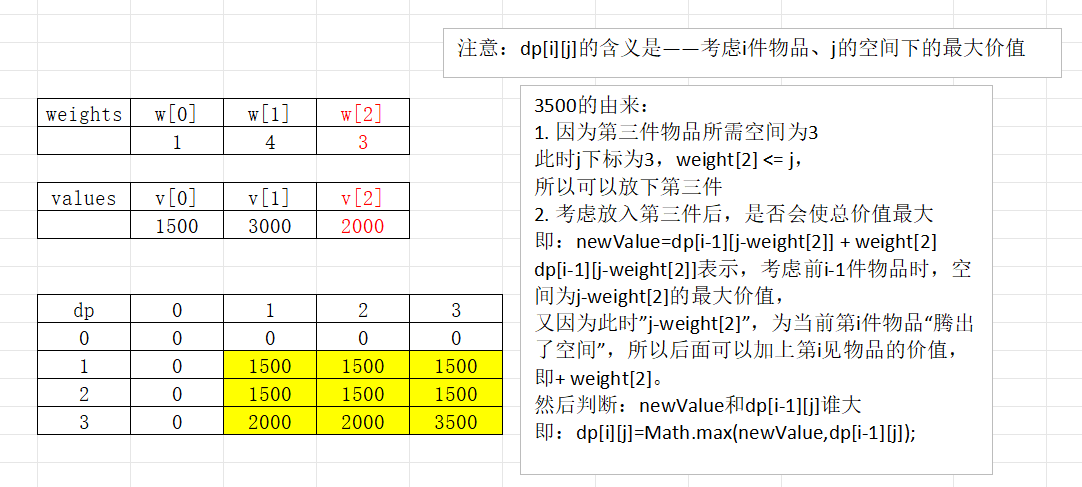
    image-20241114135349739

代码实现

KnapsackProblem

空间优化：可以通过只使用一维数组来优化空间复杂度。因为每一行的状态仅依赖于前一行的状态。（拓展）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
package com.yukinoshita.algorithm.dynamicProgramming;

import java.util.Arrays;

public class KnapsackProblem {

    public static void main(String[] args) {
        // 物品的重量
        int[] weights = {1, 4, 3};
        // 物品的价值
        int[] values = {1500, 3000, 2000};

        // 物品数量
        int numItems = weights.length;
        // 背包容量
        int capacity = 4;

        // dp[i][j] 表示考虑前 i 个物品，背包容量为 j 时能够获得的最大价值
        int[][] dp = new int[numItems + 1][capacity + 1];

        // 为了记录被放入背包的商品，定义一个二维数组
        int[][] path = new int[numItems + 1][capacity + 1];

        // 动态规划求解最大价值
        for (int i = 1; i <= numItems; i++) {
            for (int j = 1; j <= capacity; j++) {
                if (weights[i - 1] > j) { // 当前背包容量不足以放入物品 i
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 如果放入当前物品 i 会得到更大的价值，更新 dp[i][j] 和 path
                    if (dp[i - 1][j] < dp[i - 1][j - weights[i - 1]] + values[i - 1]) {
                        dp[i][j] = dp[i - 1][j - weights[i - 1]] + values[i - 1];
                        path[i][j] = 1; // 记录当前物品 i 被放入背包
                    } else {
                        dp[i][j] = dp[i - 1][j];
                    }
                }
            }
        }

        // 打印 dp 数组，查看每个容量下的最大价值
        for (int[] row : dp) {
            System.out.println(Arrays.toString(row));
        }

        // 输出最大能够装入的价值
        System.out.println("最大能装的价值为：" + dp[numItems][capacity]);

        // 输出放入背包的物品
        int i = numItems;
        int j = capacity;
        while (i > 0 && j > 0) {
            if (path[i][j] == 1) {
                System.out.printf("第%d个商品放入背包\n", i);
                j -= weights[i - 1]; // 剩余背包容量
            }
            i--; // 遍历前一个物品
        }
    }
}