深度优先搜索（DFS）

所谓图的遍历，即是对结点的访问。一个图有那么多个结点，如何遍历这些结点，需要特定策略，一般有两种访问策略: (1)深度优先遍历 (2)广度优先遍历

图的深度优先搜索（Depth First Search）

  1. 深度优先遍历，从初始访问结点出发，初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点， 可以这样理解：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
  2. 我们可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。
  3. 显然，深度优先搜索是一个递归的过程

算法步骤

  1. 访问初始结点v，并标记结点v为已访问。
  2. 查找结点v的第一个邻接结点w。
  3. 若w存在，则继续执行4，如果w不存在，则回到第1步，将从v的下一个结点继续。
  4. 若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
  5. 查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

深度优先遍历抽象图解

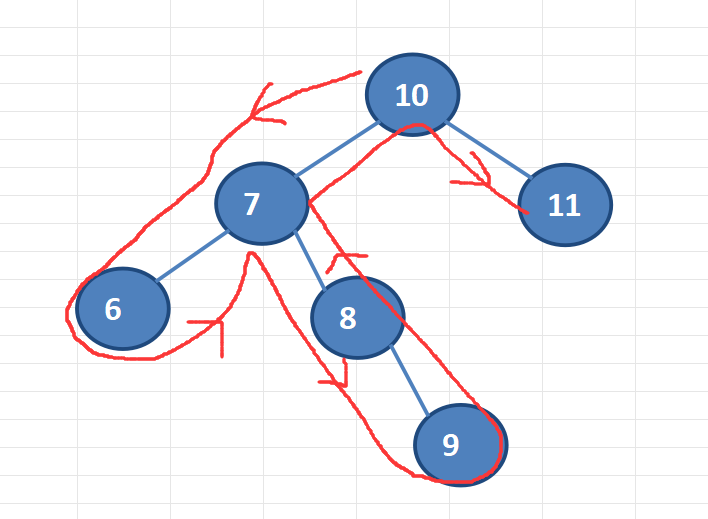
image-20241114115759159

代码实现

以此为例：

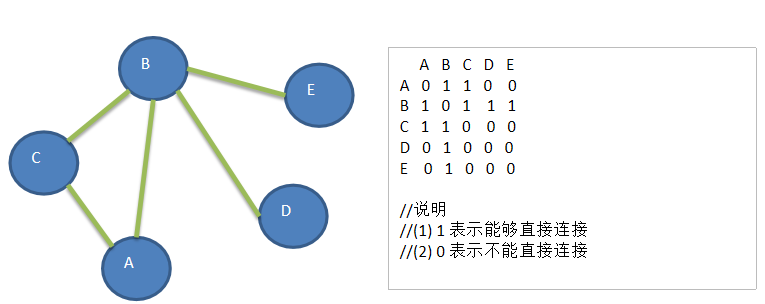
image-20241111093246143

从A开始遍历，遍历所有节点

Graph

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
package com.yukinoshita.dataStructure.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;

public class Graph {

    private ArrayList<String> vertexList;
    private int[][] edges;
    private int numOfEdges;
    //记录某个顶点是否被访问过
    private boolean[] vis;

    public static void main(String[] args) {

        int n = 5;
        String Vertexs[] = {"A", "B", "C", "D", "E"};
        Graph graph = new Graph(n);
        for (String vertex : Vertexs) {
            graph.insertVertex(vertex);
        }
        //添加边
        //A-B A-C B-C B-D B-E
        graph.insertEdge(0, 1, 1); // A-B
        graph.insertEdge(0, 2, 1); //
        graph.insertEdge(1, 2, 1); //
        graph.insertEdge(1, 3, 1); //
        graph.insertEdge(1, 4, 1); //
        graph.showGraph();

        graph.dfs();
    }

    //对dfs重载，遍历所有节点，进行dfs（确保了所有点能被访问到）
    public void dfs() {
        for(int i=0;i<getNumOfVertex();i++){
            dfs(vis, 0);
        }
    }


    //从某一个节点开始，进行深度优先搜索
    private void dfs(boolean[] visited, int i) {
        System.out.print(getValueByIndex(i) + "->");
        visited[i] = true;
        //查找节点i的第一个邻接节点
        int w = getFirstNeighbor(i);
        while (w != -1) {//说明有下一个邻接节点
            if (!visited[w]) {//再加上没有被访问过
                dfs(visited, w);
            }
            //如果w节点已经被访问过，得找下一个
            w = getNextNeighbor(i, w);
        }
    }

    /**
     * （？存疑）根据前一个邻接节点的下标来获取下一个邻接节点
     * @param v1 上一个节点的行号
     * @param v2 上一个节点的列号
     * @return 下一个节点在vertexList的下标j，没有则-1
     */
    public int getNextNeighbor(int v1, int v2) {
        for (int j = v2 + 1; j < vertexList.size(); j++) {
            if (edges[v1][j] > 0) {
                return j;
            }
        }
        return -1;
    }

    /**
     * 得到第一个邻接节点的下标
     *
     * @param index
     * @return 下一个邻接节点的下标，没有则-1
     */
    public int getFirstNeighbor(int index) {
        for (int j = 0; j < vertexList.size(); j++) {
            if (edges[index][j] > 0) {
                return j;
            }
        }
        return -1;
    }


    //构造器
    public Graph(int n) {
        edges = new int[n][n];
        vertexList = new ArrayList<String>(n);
        numOfEdges = 0;
        vis = new boolean[n];
    }

    //获取顶点数量
    public int getNumOfVertex() {
        return vertexList.size();
    }

    //展示图
    public void showGraph() {
        for (int[] link : edges) {
            System.err.println(Arrays.toString(link));
        }
    }

    //获取边的数量
    public int getNumOfEdges() {
        return numOfEdges;
    }

    //获取顶点的值
    public String getValueByIndex(int i) {
        return vertexList.get(i);
    }

    //获取权值
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }

    //插入顶点
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }

    //插入边
    public void insertEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }
}