希尔排序(经典)
思路分析
首先是关于插入排序存在的问题:

会发现当我们要插入的数据是较小的数时,后移的次数明显增多,对效率有影响
希尔排序介绍:
也是一种插入排序,他是简单插入排序经过改进后的一个更高效版本,也成为缩小增量排序
基本思想:
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法终止。
- 分组:希尔排序首先将整个待排序的数组按下标分成若干组。每组的元素之间的下标差为一个预先设定的增量(也称为“步长”)。例如,假设增量为 3,则数组中的元素会被分成多个子数组,每个子数组包含的元素是下标相差 3 的元素。
- 直接插入排序:对每组中的元素使用直接插入排序算法进行排序。直接插入排序是将待排序元素逐个插入到已排序序列中的方法,适用于小规模数据的排序。
- 减少增量:随着排序的进行,增量逐渐减少,通常会按照某种规则(如减半或减小固定值)来选择新的增量。每次减少增量后,分组的方式会发生变化,此时会有更多的元素被分到同一组中。
- 最终排序:当增量减小到 1 时,所有元素就会被视为一组,此时使用插入排序对整个数组进行排序。由于之前的分组和局部排序,整体数据已经趋近于有序,因此最后的插入排序能够更高效地完成。
- 总结:希尔排序通过先对远距离的元素进行排序,然后逐步缩小距离,使得数据逐渐接近有序,从而提高插入排序的效率。这种分组和逐步排序的方式使得希尔排序比直接插入排序在处理较大数组时效率更高。
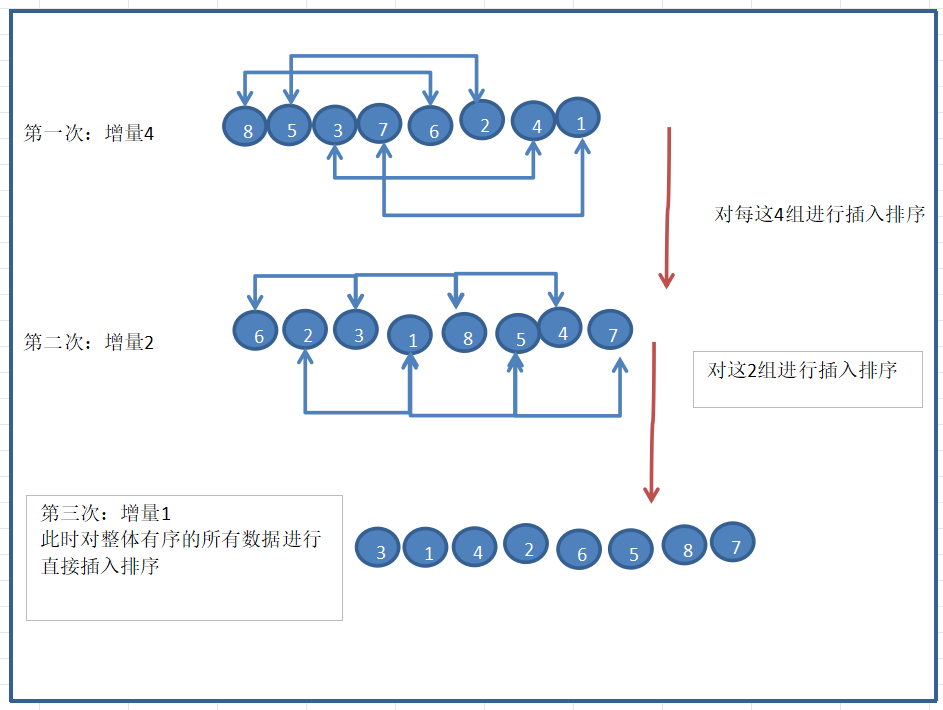
图解:
初始数组:
假设我们有一个数组:
1
| [8, 5, 3, 7, 6, 2, 4, 1]
|
选择增量:
假设我们选择初始增量为 4。数组被分为两组:
- 第一组(下标 0, 4):[8, 6]
- 第二组(下标 1, 5):[5, 2]
- 第三组(下标 2, 6):[3, 4]
- 第四组(下标 3, 7):[7, 1]
对每组进行插入排序:
对每一组进行插入排序:
- 第一组:[6, 8] → 变为
[6, 8]
- 第二组:[2, 5] → 变为
[2, 5]
- 第三组:[3, 4] → 变为
[3, 4]
- 第四组:[1, 7] → 变为
[1, 7]
整体数组变为:
1
| [6, 2, 3, 1, 8, 5, 4, 7]
|
减小增量:
将增量减小到 2。新的分组:
- 第一组(下标 0, 2, 4, 6):[6, 3, 8, 4]
- 第二组(下标 1, 3, 5, 7):[2, 1, 5, 7]
对新组进行插入排序:
- 第一组:[3, 4, 6, 8] → 变为
[3, 4, 6, 8]
- 第二组:[1, 2, 5, 7] → 变为
[1, 2, 5, 7]
整体数组变为:
1
| [3, 1, 4, 2, 6, 5, 8, 7]
|
再次减小增量:
将增量减小到 1。此时对整个数组进行插入排序:
- 最终排序结果:
1
| [1, 2, 3, 4, 5, 6, 7, 8]
|
真-上述过程的图解:
代码实现
实现1:希尔排序[交换式]
该种方法每次比较完采用了交换的方式移动数据,效率非常低:(比原生的插入排序还慢!)
(所以这种方式不能算是对插入排序的优化,只是用于演示思路比较清晰)
| 测试数据大小 |
花费时间(单位:毫秒) |
| 10000 |
71 |
| 50000 |
1419 |
| 80000 |
4179 |
| 140000 |
13005 |
ShellSort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
| package com.yukinoshita.algorithm.sort;
import java.util.Arrays;
import java.util.Random;
public class ShellSort {
public static void main(String args[]) {
int[] arr = {8, 5, 3, 7, 6, 2, 4, 1};
System.out.println("希尔排序每轮过程:");
shellDetailedSort(arr);
System.out.println("-------------下面展示shellSort--------------------");
int[] arr2 = {8, 5, 3, 7, 6, 2, 4, 1};
System.out.println("排序前:" + Arrays.toString(arr2));
shellSort(arr2);
System.out.println("排序后:" + Arrays.toString(arr2));
testPerformance();
}
private static void shellSort(int[] arr) {
for(int gap=arr.length/2;gap>0;gap/=2){
for(int i=gap;i<arr.length;i++){
for(int j=i-gap;j>=0;j-=gap){
if(arr[j]>arr[j+gap]){
int temp = arr[j];
arr[j] = arr[j+gap];
arr[j+gap] = temp;
}
}
}
}
}
private static void shellDetailedSort(int[] arr) {
for(int i=4;i<arr.length;i++){
for(int j=i-4;j>=0;j-=4){
if(arr[j]>arr[j+4]){
int temp = arr[j];
arr[j] = arr[j+4];
arr[j+4] = temp;
}
}
}
System.out.println("第一轮排序后:"+Arrays.toString(arr));
for(int i=2;i<arr.length;i++){
for(int j=i-2;j>=0;j-=2){
if(arr[j]>arr[j+2]){
int temp = arr[j];
arr[j] = arr[j+2];
arr[j+2] = temp;
}
}
}
System.out.println("第二轮排序后:"+Arrays.toString(arr));
for(int i=1;i<arr.length;i++){
for(int j=i-1;j>=0;j-=1){
if(arr[j]>arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
System.out.println("第三轮排序后:"+Arrays.toString(arr));
}
public static void testPerformance() {
int size = 10000;
int[] arr = new int[size];
Random random = new Random();
for (int i = 0; i < size; i++) {
arr[i] = random.nextInt(100000);
}
long startTime = System.currentTimeMillis();
shellSort(arr);
long endTime = System.currentTimeMillis();
System.out.println("排序大小: " + size);
System.out.println("排序时间: " + (endTime - startTime) + " 毫秒");
}
}
|
实现2:希尔排序[移动式]
真-做到了对直接插入排序的究极优化!
| 测试数据大小 |
花费时间(单位:毫秒) |
| 10000 |
3 |
| 50000 |
6 |
| 80000 |
12 |
| 140000 |
17 |
ShellSort(对上述文件进行了覆盖并修改)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| package com.yukinoshita.algorithm.sort;
import java.util.Arrays;
import java.util.Random;
public class ShellSort {
public static void main(String args[]) {
int[] arr = {8, 5, 3, 7, 6, 2, 4, 1};
System.out.println("排序前:" + Arrays.toString(arr));
shellSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
testPerformance();
}
private static void shellSort(int[] arr) {
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
int insertVal = arr[i];
int insertIndex = i - gap;
while(insertIndex>=0&&insertVal<arr[insertIndex]) {
arr[insertIndex+gap]=arr[insertIndex];
insertIndex-=gap;
}
arr[insertIndex+gap]=insertVal;
}
}
}
public static void testPerformance() {
int size = 140000;
int[] arr = new int[size];
Random random = new Random();
for (int i = 0; i < size; i++) {
arr[i] = random.nextInt(100000);
}
long startTime = System.currentTimeMillis();
shellSort(arr);
long endTime = System.currentTimeMillis();
System.out.println("排序大小: " + size);
System.out.println("排序时间: " + (endTime - startTime) + " 毫秒");
}
}
|







