堆排序(经典)

思路分析

基本介绍

  1. 堆排序是利用堆这种数据结构设计的一种算法，堆排序是一种选择排序，最坏、最好、平均时间复杂度为$0(n\log n)$，是不稳定排序。
  2. 堆是具有以下性质的完全二叉树：每个节点的值都大于等于其左右子节点的值，成为大顶堆；每个节点的值都小于等于其左右子节点的值，成为小顶堆。
  3. 大顶堆图解，以及其映射到数组的形式（前有讲顺序存储二叉树）。
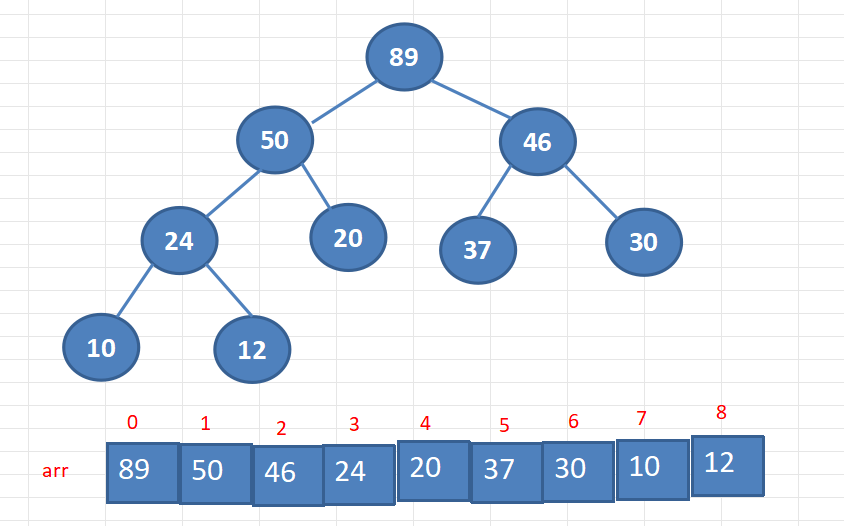
image-20241104200655911
  1. 一般升序用大顶堆，降序用小顶堆。

代码实现上：化为大顶堆形式后，通过将root沉底的方式，将最大元素放到数组末尾

基本思想

若要完成升序排序，采用大顶堆：

  1. 将待排序序列构成一个大顶堆（数组形式）。
  2. 此时，序列最大值就是堆顶的根节点。
  3. 将其与末尾元素进行交换，此时末尾就成为最大元素。
  4. 然后将剩余$n-1$个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列。

可见在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列。

上述过程，初见，抽象。图解：

思路分析（清晰版）

构造大根堆图解：

如果不能看懂，移步原文->菜鸟教程：堆的基本存储->堆的shift up->堆的shift down->基础堆排序->优化堆排序

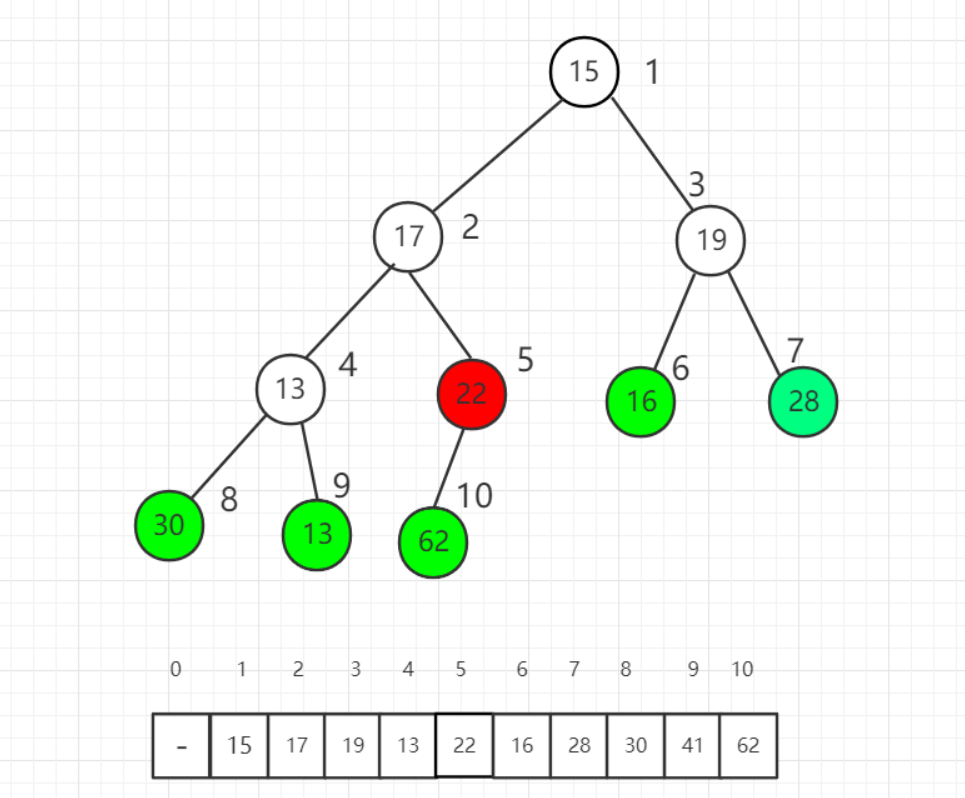
image-20241105185854553
  1. 上图为初始状态，首先利用完全二叉树的性质，得到第一个非叶子节点的位置——k = arr.length/2，也就是下标为5，值为22的节点（二叉树只是为了便于理解，实际存储方式是顺序），上图可见：只要1<=i<=5这个范围内的，都需要进行调整。目前这一步先对5这棵子树进行调整。

  • 调整：对应堆的shift up，这里简单说明一下：

    比较当前节点与其左右子节点的大小关系，找到最大的那个与当前节点交换（这里是5号与10号进行交换）

  1. 第一步调整完结果如下。提示：节点标绿表示不需要再被操作的节点，标红表示当前要继续操作的节点：
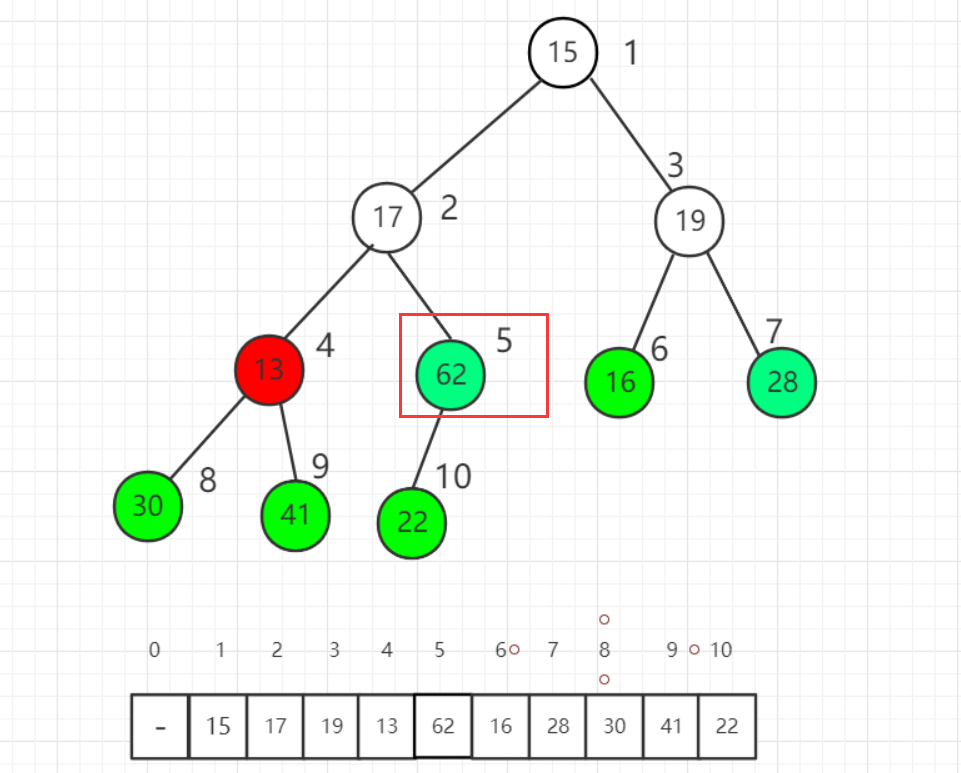
image-20241105190611082
  1. 同样道理的，对4号节点进行同样的调整。需要将4号与9号交换位置。
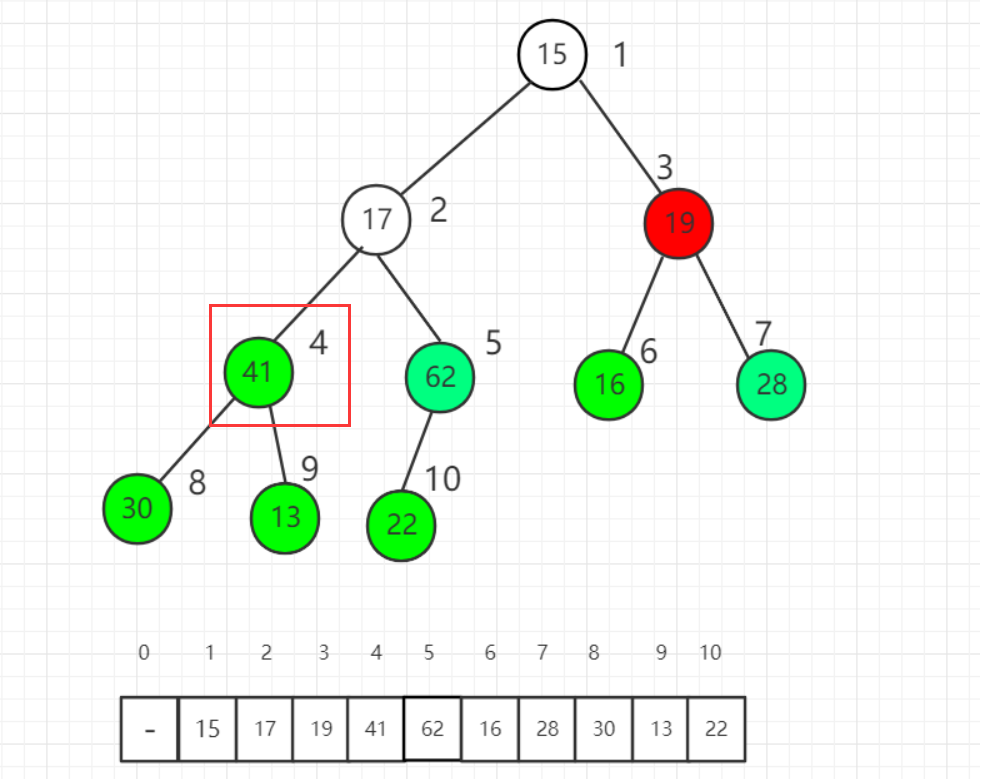
image-20241105190918145
  1. 对3号操作，需要将3号与7号交换：（原图没标绿……手动标一下……）
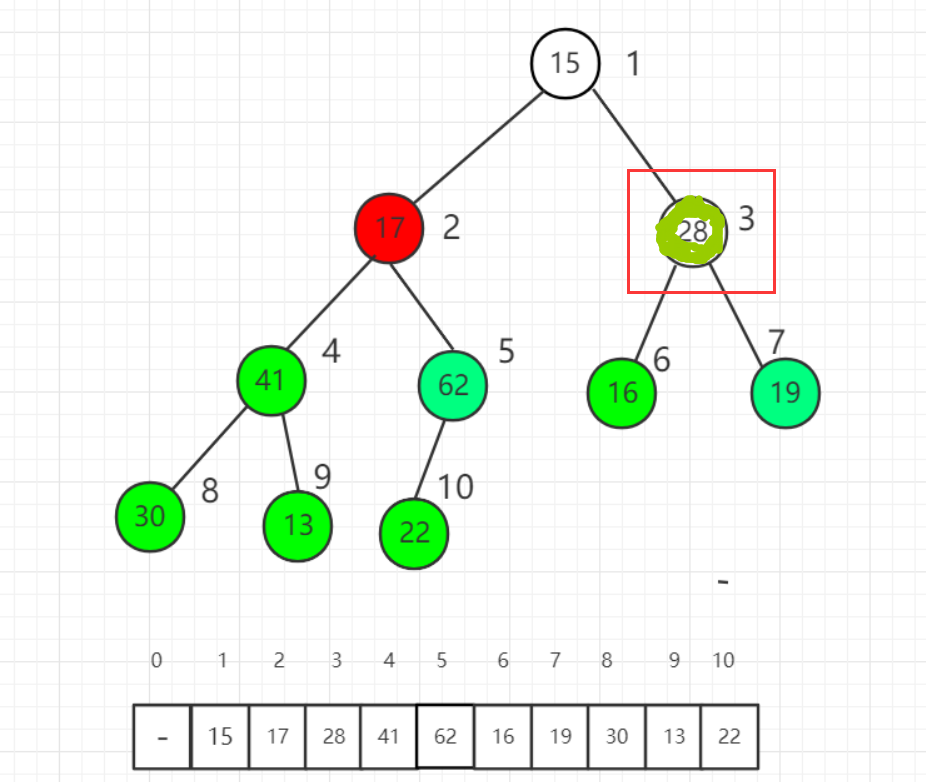
image-20241105191115658
  1. 对2号操作，将2号于5号交换：
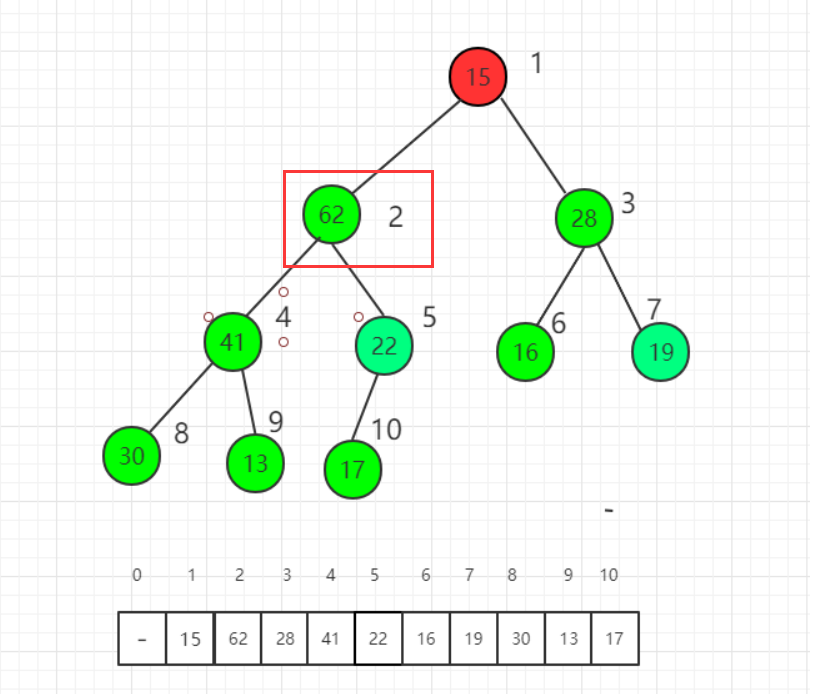
image-20241105191218231
  1. 最后对1号，也就是根节点进行调整，实现了一个大顶堆：
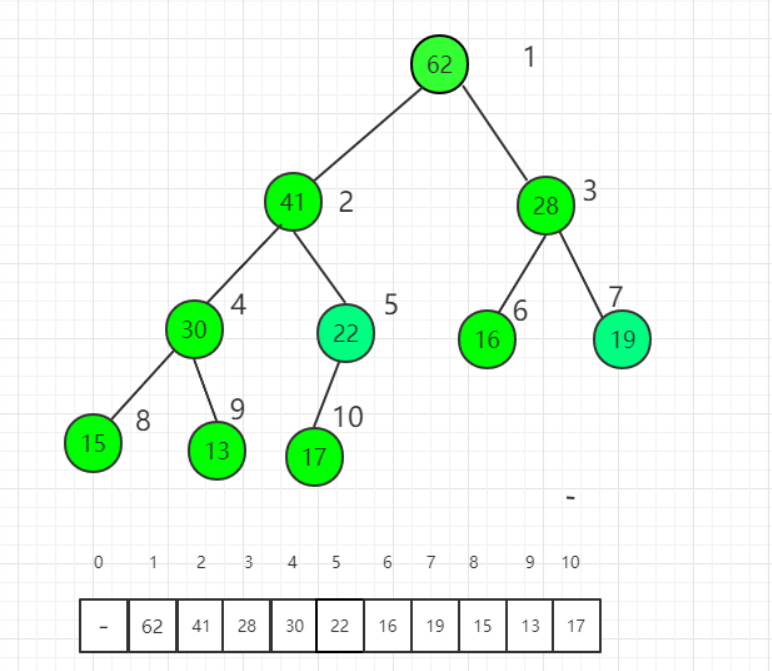
image-20241105191311699

思路对应代码部分：

上述思路的调整，对应代码的adjustHeap方法，

而对于从第一个非叶子节点处理到根节点的代码为:

1
2
3
4
for(int i=arr.length/2;i>=0;i--){
    //调整操作
    adjustHeap(arr,i,arr,length);
}

上述过程调整为一个大顶堆的操作应该能理解了，但最终目的还是为了实现对整个数组的升序排序，大顶堆只是这个过程用到的工具。

后续操作参考优化堆排序。将堆顶最大元素与末尾元素交换，但是此时破坏了大顶堆的结构，我们可以利用已写好的adjustHeap方法，从上至下，可以对照二叉树来看，也可以看数组：

注意：

代码部分：

1
2
3
4
5
6
for(int j= arr.length-1;j>0;j--){
            temp = arr[j];//将底部元素与顶部元素交换
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, j);
        }

我们每交换一次首尾，仅使用一次adjustHeap就可以把整个结构重新调整回大顶堆，理由是：交换完最大元素和末尾元素后，整个结构本身就是很有序的，换句话说，除了根节点，其他的子树都符合"大顶堆"的结构（父节点大于其左右子节点）。

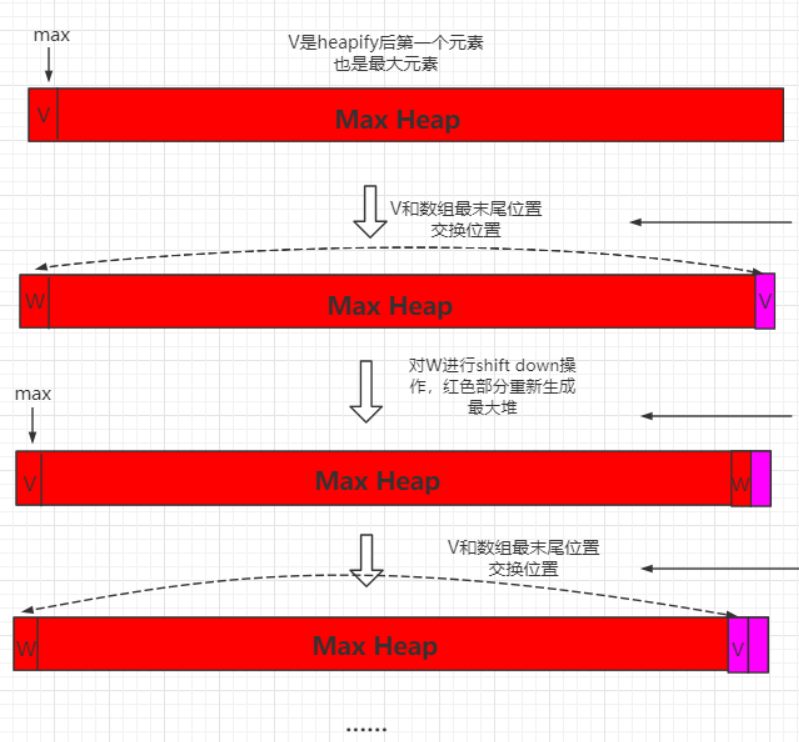
image-20241105192344775

至此，解释完了所有的代码，再不理解，就静下来慢慢看，或者看看别的文章（这些文章我还没看，虽然都找了，但是光看菜鸟就看懂了博客1、博客2、博客3），或者代码debug看看，或者画图一步步走下去，或者……

代码实现

测试数据大小 花费时间（单位：毫秒）
10000 1
50000 5
80000 8
140000 13
500000 46
900000 83

HeapSort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
package com.yukinoshita.algorithm.sort;

import java.util.Arrays;

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {4,6,8,5,9};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void heapSort(int[] arr) {
        int temp = 0;
        //分步演示：
//        adjustHeap(arr,1,arr.length);
//        adjustHeap(arr,0,arr.length);

        for(int i = arr.length/2 - 1; i >= 0; i--) {
            adjustHeap(arr, i, arr.length);
        }

        for(int j= arr.length-1;j>0;j--){
            temp = arr[j];//将底部元素与顶部元素交换
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, j);
        }
    }

    /**
     * 将以i对应的非叶子节点的树调整成大顶堆
     *
     * @param arr    待调整的数组
     * @param i      表示非叶子节点在数组中索引
     * @param length 表示对多少个元素进行调整,length逐渐减少
     */
    public static void adjustHeap(int[] arr, int i, int length) {
        int temp = arr[i];

        //k=2*i+1 是指节点i的左子节点
        for (int k = 2 * i + 1; k < length; k = k * 2 + 1) {
            if (k + 1 < length && arr[k] < arr[k + 1]) {//左子节点小于右子节点
                k++;
            }
            if (arr[k] > temp) {//子节点大于父节点
                arr[i] = arr[k];
                i = k;//i变为k，继续循环比较
            } else {
                break;
            }
        }
        //for循环结束，已经将以i为父节点的树的最大值，放在了最顶（局部）
        arr[i] = temp;//将temp放到调整后的位置
    }

}