并查集

由于目录编排原因，好像并查集是图？并不是，它是一种独立的抽象的数据结构。可以看做是一棵树或森林。

并查集的定义以及算法实现参考了OI WIKI并查集以及blog提供了形象生动的例子。

同时参考了GPT所提供应用、代码。

基本介绍：

并查集(DSU)，全称为Disjoint Set Union。

  1. 并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

  2. 顾名思义，并查集支持两种操作：

    • 合并（Union）：合并两个元素所属集合（合并对应的树）

    • 查询（Find）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

    删除、移动属于扩展的操作，需要将parent数组增加值两倍，还新增一个size[]来记录每个集合中元素个数，其大小也是两倍。

    • 通常情况下并查集的标准实现只需要find和unite就行，如需扩展功能才将数组空间变为两倍，因此也给出两种代码。

并查集的应用：

  1. 连通性问题
    • 并查集最经典的应用之一是判断图中节点是否连通。假设你有一个无向图，需要动态地判断两个节点是否属于同一个连通块，或者在图中添加边并进行连通性判断。并查集通过“合并”和“查找”操作，能够在近乎常数时间内解决这一问题。
    • 判断两个城市是否在同一条道路网络中。
    • 判断两个计算机是否在同一个局域网中。
  2. 最小生成树
    • 并查集是 Kruskal 算法的核心部分。Kruskal 算法通过对边进行排序并逐步合并节点，最终得到图的最小生成树。在这个过程中，使用并查集判断两个节点是否属于同一集合，防止产生环。
    • 计算带权图的最小生成树，最小成本的通信网络布设。
  3. 动态连通性
    • 在一些实时问题中，可能会动态地增加边或删除边。并查集可以高效地处理这种动态连通性的问题，例如：在某些社交网络中判断两个人是否处于同一网络中，或者当一条连接断开时判断网络是否仍然连通。
    • 判断社交网络中两个用户是否在同一个群组。
    • 判断计算机网络中两个节点是否能通信。
  4. 图的环形检测
    • 在图的遍历过程中，环的检测是一个常见问题。利用并查集可以高效地检测图中是否有环。当你尝试合并两个已经在同一集合中的节点时，说明已经发现了一个环。
    • 判断一个无向图中是否存在环。
    • 判断一个任务依赖图中是否存在循环依赖。
  5. 分割问题
    • 在图中，分割或切割的目标是将图分割成多个连通块。并查集可以帮助快速地找到哪些节点属于同一块，从而实现图的分割。
    • 网络中的分区，找到某些节点之间的最大割集。
    • 计算机科学中的图像分割问题。
  6. 动态连通性与并查集扩展
    • 一些复杂的动态连通性问题，可以使用并查集的扩展版本进行处理。例如，在动态树形结构的查询和更新中，可以通过并查集进行高效操作。
    • 在数据流中，快速查询和更新不同数据块之间的连接关系。
  7. 岛屿问题
    • 给定一个二维矩阵，其中每个元素表示一个格子，格子值为 1 表示陆地，0 表示水域。通过并查集，可以快速求解岛屿的个数，即求连通的陆地块的个数。
    • 在一个地图中，找到所有孤立的岛屿区域。
  8. 动态查询最小生成树
    • 并查集也可以用于处理某些动态修改图的问题，如在某些图的边权改变时，需要动态查询和更新最小生成树。通过与其他算法结合，保持并查集的结构可以高效更新图中的连通信息。

算法实现思路：

  1. 初始化

  2. 查询find

    1. 我们需要沿着树向上移动，直至找到根节点。

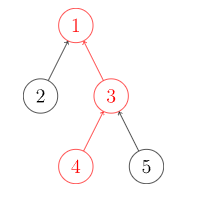
      image-20241113105235769

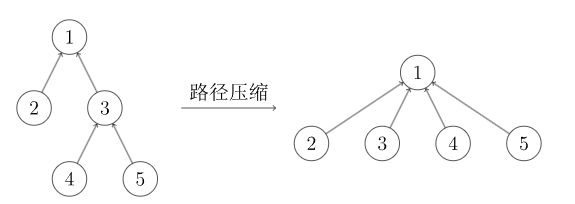
    2. 路径压缩，可以加快后续的查找速度。

      image-20241113105250975

  3. 合并

    要合并两棵树，我们只需要将一棵树的根节点连到另一棵树的根节点。

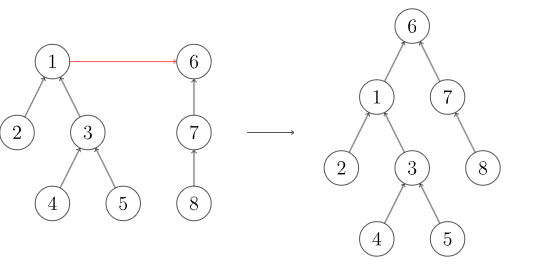
    image-20241113105355926

    补充：启发式合并

    合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以将节点较少或深度较小的树连到另一棵，以免发生退化。

  4. 删除erase

    要删除一个叶子节点，我们可以将其父亲设为自己。为了保证要删除的元素都是叶子，我们可以预先为每个节点制作副本，并将其副本作为父亲。

    实际上，这里的删除操作，只是将该元素的parent指向他自己。

    • 该操作的效果是 “断开” 元素 x 与它原来集合的联系，使 x 成为一个新的单元素集合，但并没有真正删除 x 本身，也没有改变其它集合的结构。

    • 这意味着，x 会从原集合中“移除”，但其索引仍然存在于数据结构中。换句话说，erase 操作并没有修改 parent 数组的大小，也没有真正从数据结构中“删除”元素，只是把 x 从原来的集合中分离出来。

    • 为什么？

      • 这样的设计通常用于 懒惰删除（lazy deletion）或者当需要在集合中分割元素时。这种方式避免了删除元素时可能出现的性能开销，特别是在处理大数据结构时。

      • 另外，erase 操作本身可能用于某些特定场景，比如让元素独立出来，变成一个单独的集合，供后续操作使用。

    • 进一步改进：

      • 如果需要完全删除某个元素并从集合中移除，可以考虑设计一个额外的机制来真正删除元素，可能会涉及到管理集合中实际元素的列表或数组。

  5. 移动

    与删除类似，通过以副本作为父亲，保证要移动的元素都是叶子。

带权并查集：

我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而解决更多的问题。

比如对于经典的「NOI2001」食物链，我们可以在边权上维护模 3 意义下的加法群。

标准并查集实现

DSUDemo

感谢GPT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
package com.yukinoshita.dataStructure.dsu;

import java.util.Arrays;

public class DSUDemo {
    public static void main(String[] args) {
        // 创建一个包含 5 个元素的并查集
        DSU dsu = new DSU(5);

        // 打印初始状态
        System.out.println("Initial state:");
        dsu.print();

        // 合并集合
        dsu.unite(0, 1);  // 将 0 和 1 合并
        dsu.unite(1, 2);  // 将 1 和 2 合并
        dsu.unite(3, 4);  // 将 3 和 4 合并

        // 打印合并后的状态
        System.out.println("After uniting (0,1), (1,2), (3,4):");
        dsu.print();

        // 查找操作
        System.out.println("Find root of 0: " + dsu.find(0));  // 输出 0 或 2，因为 0 和 2 在同一个集合中
        System.out.println("Find root of 4: " + dsu.find(4));  // 输出 4 或 3，因为 3 和 4 在同一个集合中

        // 再次合并 2 和 3
        dsu.unite(2, 3);  // 将 2 和 3 合并

        // 打印合并后的状态
        System.out.println("After uniting (2,3):");
        dsu.print();

        // 查找操作
        System.out.println("Find root of 0: " + dsu.find(0));  // 输出 2
        System.out.println("Find root of 4: " + dsu.find(4));  // 输出 2，因为 4 通过 3 和 2 连接到一起
    }
}

class DSU {
    int[] parent;  // 用于存储每个元素的父节点
    int[] size;    // 用于存储每个集合的大小

    // 构造函数：初始化并查集，设置每个元素的父节点为自己，集合大小为 1
    public DSU(int size_) {
        parent = new int[size_];
        size = new int[size_];

        // 初始化，父节点指向自己，集合大小为 1
        for (int i = 0; i < size_; i++) {
            parent[i] = i;    // 每个元素的父节点初始化为它自己
            size[i] = 1;      // 每个集合的初始大小为 1
        }
    }

    // 查找操作：返回元素 x 所在集合的根节点，同时使用路径压缩优化
    public int find(int x) {
        // 如果 x 的父节点是它自己，说明它是根节点，直接返回
        // 否则递归查找其父节点并进行路径压缩
        return x == parent[x] ? x : (parent[x] = find(parent[x]));
    }

    // 合并操作：将元素 x 和 y 所在的集合合并
    public void unite(int x, int y) {
        // 查找元素 x 和 y 的根节点
        int rootX = find(x);
        int rootY = find(y);

        // 如果 x 和 y 已经在同一个集合中，则不需要合并
        if (rootX != rootY) {
            // 根据集合大小来决定将哪个集合合并到另一个集合
            if (size[rootX] < size[rootY]) {
                parent[rootX] = rootY;  // 将 x 所在的集合合并到 y 所在的集合
                size[rootY] += size[rootX];  // 更新 y 所在集合的大小
            } else {
                parent[rootY] = rootX;  // 将 y 所在的集合合并到 x 所在的集合
                size[rootX] += size[rootY];  // 更新 x 所在集合的大小
            }
        }
    }

    // 打印当前并查集的父节点数组和集合大小数组
    public void print() {
        System.out.println("Parent: " + Arrays.toString(parent));  // 打印每个元素的父节点
        System.out.println("Size: " + Arrays.toString(size));      // 打印每个集合的大小
    }
}

扩展并查集实现

ExtendedDSUDemo

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
package com.yukinoshita.dataStructure.extendedDsu;

import java.util.Arrays;

public class ExtendedDSUDemo {
    public static void main(String[] args) {
        DSU dsu = new DSU(5);
        dsu.print();
        dsu.unite(0, 1);
        dsu.unite(1, 2);
//        dsu.find(2);
        dsu.print();//此时输出parent[5,5,7,8,9,5,5,5,8,9]为什么呢？
                    //发现第2个元素和7号元素的父节点都应该是5才对？
                    //因为此时刚完成合并，没有进行过find，所以路径没压缩，只要加上那句注释掉的find，此时的parent[2]也会变成5
        dsu.move(0, 3);  // 将元素 0 移动到元素 3 所在的集合
        dsu.print();
    }
}

class DSU {
    int[] parent;
    int[] size;

    public DSU(int size_) {
        parent = new int[size_ * 2];
        size = new int[size_ * 2];

        // 初始化前半部分，元素属于不同的集合
        for (int i = 0; i < size_; i++) {
            parent[i] = i + size_;  // 初始化 parent 数组，前 size_ 个元素依次为 size_ 到 2*size_-1
            size[i] = 1;            // 每个集合的初始大小为 1
        }

        // 初始化后半部分，元素是自己的父节点
        for (int i = size_; i < size_ * 2; i++) {
            parent[i] = i;          // 后半部分，pa[i] = i，表示每个元素自己是根
            size[i] = 1;            // 初始集合大小为 1
        }
    }

    // 查找并进行路径压缩
    public int find(int x) {
        return x == parent[x] ? x : (parent[x] = find(parent[x]));
    }

    // 合并两棵树，按大小合并
    public void unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        // 如果两个元素已经在同一个集合中，直接返回
        if (rootX != rootY) {
            // 按大小合并：将小树合并到大树下
            if (size[rootX] < size[rootY]) {
                parent[rootX] = rootY;
                size[rootY] += size[rootX];
            } else {
                parent[rootY] = rootX;
                size[rootX] += size[rootY];
            }
        }
    }

    // 将元素 x 移动到元素 y 所在的集合
    public void move(int x, int y) {
        int fx = find(x);  // 查找元素 x 所在的集合的根
        int fy = find(y);  // 查找元素 y 所在的集合的根

        // 如果 x 和 y 已经在同一个集合中，不需要移动
        if (fx == fy) return;

        // 将 x 移动到 y 所在的集合
        parent[x] = fy;  // 让 x 的父节点指向 y 所在的集合
        size[fx]--;      // 原集合的大小减 1
        size[fy]++;      // 目标集合的大小加 1
    }

    // 打印 parent 和 size 数组的状态
    public void print() {
        System.out.println("Parent: " + Arrays.toString(parent));
        System.out.println("Size: " + Arrays.toString(size));
    }
}